题目内容
【题目】已知函数![]() ,有下列四个命题:
,有下列四个命题:
①函数![]() 是奇函数;
是奇函数;
②函数![]() 在
在![]() 是单调函数;
是单调函数;
③当![]() 时,函数
时,函数![]() 恒成立;
恒成立;
④当![]() 时,函数
时,函数![]() 有一个零点,
有一个零点,
其中正确的是____________
【答案】③④
【解析】
①根据![]() 与
与![]() 的关系即可判断;②当
的关系即可判断;②当![]() 时,
时,![]() ,对
,对![]() 求导可得
求导可得![]() ,设
,设![]() ,显然
,显然![]() 连续,利用零点存在性定理可得存在
连续,利用零点存在性定理可得存在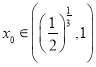 ,使得
,使得![]() ,即可判断
,即可判断![]() 时
时![]() 的单调性,进而判断②;由②可知当
的单调性,进而判断②;由②可知当![]() 时,
时,![]() 为
为![]() 的最小值,判断
的最小值,判断![]() 是否成立即可判断③;利用零点存在性定理即可判断④.
是否成立即可判断③;利用零点存在性定理即可判断④.
由题,![]() 的定义域为
的定义域为![]() ,
,
①![]() ,且
,且![]() ,所以
,所以![]() 不是奇函数,故①错误;
不是奇函数,故①错误;
②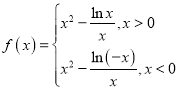 ,当
,当![]() 时,
时,![]() ,
,
则![]() ,
,
令![]() ,则
,则![]() ,
,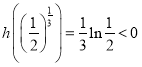 ,
,
所以存在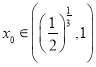 ,使得
,使得![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 是单调减函数;
是单调减函数;
当![]() 时,
时,![]() ,
,![]() 是单调增函数,
是单调增函数,
所以②错误;
③由②可知,当![]() 时,
时,![]() 在
在![]() 上有最小值,且
上有最小值,且![]() ,
,
所以![]() ,
,
因为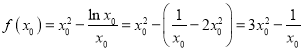 ,
,
由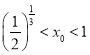 ,则
,则![]() ,即
,即![]() ,
,
所以![]() ,
,
所以当![]() 时,
时,![]() 恒成立,故③正确;
恒成立,故③正确;
④当![]() 时,
时,![]() ,且
,且![]() ,
,![]() ,
,
所以![]() 在
在![]() 内有一个零点,故④正确.
内有一个零点,故④正确.
故答案为:③④

练习册系列答案
相关题目