Question

【题目】选修4-5：不等式选讲

已知函数.

（Ⅰ）若，解不等式；

（Ⅱ）当时，函数的最小值为，求实数的值.

Answer 1

【答案】(Ⅰ) (Ⅱ)

【解析】

（Ⅰ）a=-2时， ，f(x)的两个零点分别为-1和1，通过零点分段法分别讨论 ，去绝对值解不等式，最后取并集即可；

（Ⅱ）法一： 时， ，化简f(x)为分段函数，根据函数的单调性求出f(x)在 处取最小值3，进而求出a值。法二：先放缩，再由绝对值三角不等式求出f(x)最小值，进而求a。

(Ⅰ) 时，不等式为

①当 时，不等式化为，，此时

②当 时，不等式化为，

③当 时，不等式化为，，此时

综上所述，不等式的解集为

（Ⅱ）法一：函数f(x)＝|2x－a|＋|x－1|，当a＜2，即时，

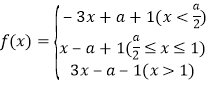
所以f(x)min＝f（）＝－＋1＝3，得a＝－4＜2(符合题意)，故a＝－4.

法二：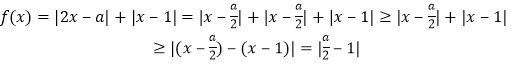

所以，又，所以.