题目内容
已知函数 ,满足:①对任意
,满足:①对任意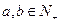 ,都有
,都有
 ;
;
②对任意n∈N *都有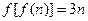 .
.
(Ⅰ)试证明: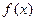 为
为 上的单调增函数;
上的单调增函数;
(Ⅱ)求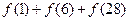 ;
;
(Ⅲ)令 ,试证明:
,试证明:
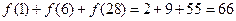
解析

练习册系列答案
相关题目
若

 ,
, ,则
,则 的大小关系为( )
的大小关系为( )
A. | B. | C. | D. |
题目内容
已知函数 ,满足:①对任意
,满足:①对任意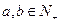 ,都有
,都有
 ;
;
②对任意n∈N *都有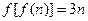 .
.
(Ⅰ)试证明: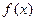 为
为 上的单调增函数;
上的单调增函数;
(Ⅱ)求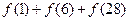 ;
;
(Ⅲ)令 ,试证明:
,试证明:
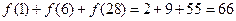
解析

若

 ,
, ,则
,则 的大小关系为( )
的大小关系为( )
A. | B. | C. | D. |