题目内容
已知a≠0,b≠0,且a
思路解析:此题考查反证法和向量共线的充要条件的证明.要证明两向量不平行,可以先假设平行,然后根据条件推出与已知矛盾的地方,从而否定假设肯定原结论.
证明:设a=(x1,y1),b=(x2,y2),a+b=(x1+x2,y1+y2),a-b=(x1-x2,y1-y2).
假设(a+b)∥(a-b),则(x1+x2)(y1-y2)-(y1+y2)(x1-x2)=0,
即x1y1+x2y1-x1y2-x2y2-x1y1-x2y2+x2y1+x2y2=0.
整理得2(x2y1-x1y2)=0,
即x2y1-x1y2=0.
∵a≠0,b≠0,
∴a∥b,这与已知a![]() b矛盾.故(a+b)
b矛盾.故(a+b)![]() (a-b).
(a-b).

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
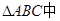 ,已知A(-
,已知A(-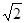 ,0),
B(
,0),
B( AB于D,
AB于D, 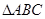 的垂心为H,且
的垂心为H,且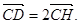

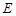 于不同的两点
于不同的两点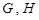 (点
(点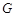 在F,H之间),且满足
在F,H之间),且满足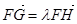 ,求
,求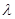 的取值范围.
的取值范围.