题目内容
(本小题满分1 0分)选修4-1:几何证明选讲
0分)选修4-1:几何证明选讲
如图,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C
作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M。
(I)求证:DC是⊙O的切线;
(II)求证:AM:MB=DF·DA。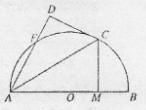
 0分)选修4-1:几何证明选讲
0分)选修4-1:几何证明选讲如图,AB是⊙O的直径,C、F为⊙O上的点,CA是∠BAF的角平分线,过点C
作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M。
(I)求证:DC是⊙O的切线;
(II)求证:AM:MB=DF·DA。
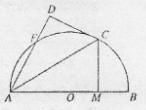
略
⑴证明:连接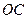 ,
,
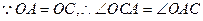 ,
,
又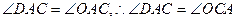 .
.
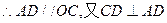 ,
,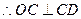 ,即
,即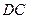 是⊙O的切线. …… 5分
是⊙O的切线. …… 5分
⑵证明:因为CA是∠BAF的角平分线,
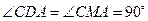 ,所以
,所以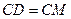 .
.
由⑴知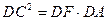 ,又
,又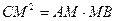 .
.
所以AM·MB=DF·DA . ………………………………10分
. ………………………………10分
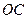 ,
,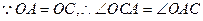 ,
,又
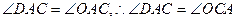 .
.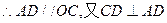 ,
,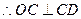 ,即
,即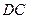 是⊙O的切线. …… 5分
是⊙O的切线. …… 5分⑵证明:因为CA是∠BAF的角平分线,
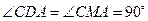 ,所以
,所以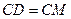 .
.由⑴知
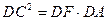 ,又
,又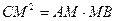 .
.所以AM·MB=DF·DA
 . ………………………………10分
. ………………………………10分
练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
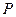 为圆
为圆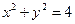 上的动点,且
上的动点,且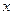 轴上,
轴上,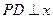 轴,垂足为
轴,垂足为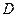 ,线段
,线段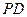 中点
中点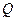 的轨迹为曲线
的轨迹为曲线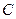 ,过定点
,过定点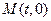
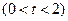 任作一条与
任作一条与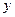 轴不垂直的直线
轴不垂直的直线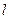 ,它与曲线
,它与曲线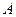 、
、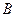 两点。
两点。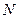 ,使得
,使得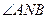 总能被
总能被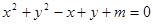 表示一个圆,则m的取值范围是 ( )
表示一个圆,则m的取值范围是 ( )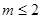
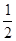
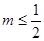

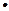 EA.
EA. 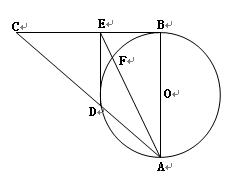
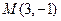 ,且与圆
,且与圆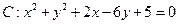 相切于点
相切于点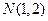 的圆的方程。
的圆的方程。 经过点P(-2,1),且点A(-1,-2)到
经过点P(-2,1),且点A(-1,-2)到