题目内容
选修4-1:几何证明选讲如图,在Rt⊿ABC中,AB=BC,以AB为直径的⊙O
交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF EA.
EA. 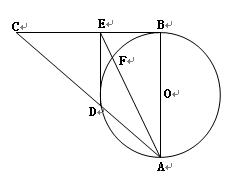
交AC于D,过D作DE⊥BC,垂足为E,连接AE交⊙O于点F,求证:CE2=EF
 EA.
EA. 
证明:在Rt⊿ABC中,∠ABC=900,
∴OB⊥CB,∴CB为⊙O的切线,
∴EB2=EF﹒EA连接BD,因为AD是⊙O的直径,
∴BD⊥AC,又因为AB=BC,所以AD=BD=DC,
∵DE⊥BC,所以BE="CE, " 所以CE2=EF﹒EA
∴OB⊥CB,∴CB为⊙O的切线,
∴EB2=EF﹒EA连接BD,因为AD是⊙O的直径,
∴BD⊥AC,又因为AB=BC,所以AD=BD=DC,
∵DE⊥BC,所以BE="CE, " 所以CE2=EF﹒EA
略

练习册系列答案
相关题目
 0分)选修4-1:几何证明选讲
0分)选修4-1:几何证明选讲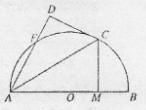
 上,与x轴的另一个交点为A,△MOA为等腰直角三角形,求圆M的方程.
上,与x轴的另一个交点为A,△MOA为等腰直角三角形,求圆M的方程.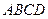 内,两个圆
内,两个圆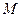 、
、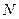 分别与矩形两边相切,且两圆互相外切。若矩形的长和宽分别为
分别与矩形两边相切,且两圆互相外切。若矩形的长和宽分别为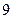 和
和 ,试把两个圆的面积之和
,试把两个圆的面积之和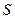 表示为圆
表示为圆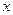 的函数关系式,并求
的函数关系式,并求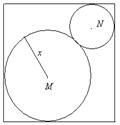
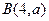 且与x轴相切的圆只有一个,求
且与x轴相切的圆只有一个,求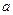 的值及圆的方
的值及圆的方 程.
程.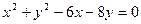 ,设该圆过点
,设该圆过点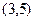 的最长弦和最短弦分别为
的最长弦和最短弦分别为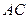 和
和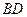 ,则四边形
,则四边形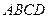 的面积为 ( )
的面积为 ( )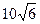
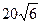
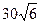
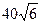
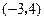 为圆心,且与
为圆心,且与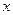 轴相切的圆的方程是( )
轴相切的圆的方程是( )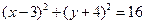

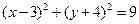
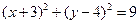
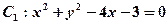 和
和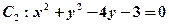 的交点的圆方程
的交点的圆方程
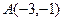 和
和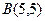 为直径端点的圆的方程是 ;
为直径端点的圆的方程是 ;