��Ŀ����
����Ŀ��ij����̨����һ���������͵����ֽ�Ŀ��A��B���Ӹ�������ѡ�ֲ��������������ֵı����ɼ���Ϊ�������ݣ����Ƴɾ�Ҷͼ��ͼ��ʾ��Ϊ�����ӽ�Ŀ��Ȥζ�ԣ������˹��⽫A�ӵ���λѡ�ֵijɼ�û�и��������Ҹ�֪���B�ӵ�ƽ���ֱ�A�ӵ�ƽ���ֶ�4�֣�ͬʱ�涨���ijλѡ�ֵijɼ�������21�֣����á��������� 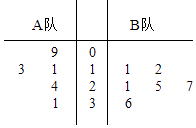
��1�����ݾ�Ҷͼ�е����ݣ����A�ӵ���λѡ�ֵijɼ���
��2�������˴�A������ѡ�ֳɼ��������2������������һ��Ϊ���������ĸ��ʣ�
��3�������˴�A��B��������ѡ�ֳɼ��ֱ������ȡ2�����dz�ȡ����������ѡ�ֵ�������Ϊ�Σ���εķֲ��м���ѧ������
���𰸡�
��1���⣺��A�ӵ���λѡ�ֵijɼ�Ϊx��
������ã� ![]() ��9+11+13+24+31+x=
��9+11+13+24+31+x= ![]() ��11+12+21+25+27+36����
��11+12+21+25+27+36����
���x=20��
��A�ӵ���λѡ�ֵijɼ�Ϊ20��
��2���⣺�ɣ�1��֪A��6λѡ���гɼ�������21�ֵ���2λ����A��6λѡ������2�˻�á���������
�����˴�A������ѡ�ֳɼ��������2���������¼�����n= ![]() =15��
=15��
������һ��Ϊ���������ĸ���p=1�� ![]() =
= ![]() ��
��
��3���⣺������A��6λѡ������2�˻�á���������B��6λѡ������4�˻�á���������
�����˴�A��B��������ѡ�ֳɼ��ֱ������ȡ2�����dz�ȡ����������ѡ�ֵ�������Ϊ�Σ�
��εĿ���ȡֵΪ0��1��2��3��4��
P����=0��= ![]() =
= ![]() ��
��
P����=1��= ![]() +
+ ![]() =
= ![]() ��
��
P����=2��= ![]() +
+ ![]() +
+ ![]() =
= ![]() ��
��
P����=3��= ![]() +
+ ![]() =
= ![]() ��
��
P����=4��= ![]() =
= ![]() ��
��
��εķֲ���Ϊ��
�� | 0 | 1 | 2 | 3 | 4 |
P | | | | | |
E��= ![]() +3��
+3�� ![]() +4��
+4�� ![]() =2��
=2��
����������1����A�ӵ���λѡ�ֵijɼ�Ϊx�����þ�Ҷͼ��ƽ�����Ķ��������A�ӵ���λѡ�ֵijɼ�����2��A��6λѡ������2�˻�á��������������˴�A������ѡ�ֳɼ��������2��������������¼����������ɶ����¼����ʼ��㹫ʽ�����������һ��Ϊ���������ĸ��ʣ���3��������A��6λѡ������2�˻�á���������B��6λѡ������4�˻�á�����������εĿ���ȡֵΪ0��1��2��3��4���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��м���ѧ������
�����㾫����������Ŀ����֪����������Ƶ�ʷֲ�ֱ��ͼ����ɢ�������������ֲ��е����֪ʶ���Եõ�����Ĵ𰸣���Ҫ����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ�����������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��У�


