题目内容
(满分14分)设函数 .若方程
.若方程 的根为0和2,且
的根为0和2,且 .
.
(1). 求函数 的解析式;
的解析式;
(2) 已知各项均不为零的数列 满足:
满足: 为该数列的前n项和),求该数列的通项
为该数列的前n项和),求该数列的通项 ;
;
(3)如果数列 满足
满足 .求证:当
.求证:当 时,恒有
时,恒有 成立.
成立.
【答案】
(1)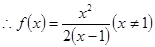 ;(2)
;(2) 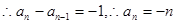 ;
;
(3) 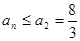
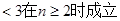 .
.
【解析】
(1)根据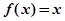 的根为0和2,借助韦达定理可建立关于a,b的方程,再根据
的根为0和2,借助韦达定理可建立关于a,b的方程,再根据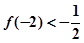 ,可确定出c值,从而求出a,b 的值,确定f(x)的解析式.
,可确定出c值,从而求出a,b 的值,确定f(x)的解析式.
(2) 由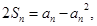 得
得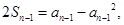 然后两个式子作差可得到
然后两个式子作差可得到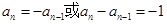 ,再根据条件排除
,再根据条件排除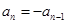 ,从而确定
,从而确定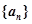 为等差数列,问题得解.
为等差数列,问题得解.
(3)解本小题的关键是由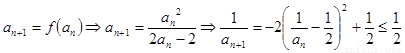 ,
,
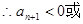
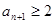 .然后再分两种情况讨论求解.
.然后再分两种情况讨论求解.
解:(1)设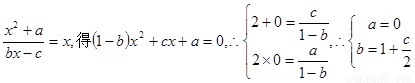 …2分
…2分
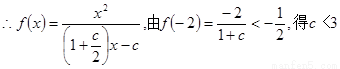 ,又
,又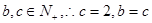
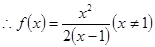 ……4分
……4分
(2)由已知得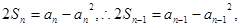 ……5分
……5分
两式相减得 ,
,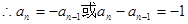 ……6分
……6分
当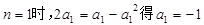 .若
.若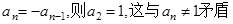
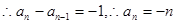 ……8分
……8分
(3) 由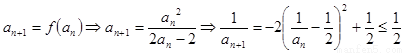 ,……10分
,……10分
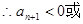
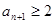 .……11分
.……11分
若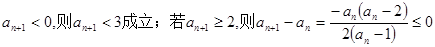 ……13分
……13分
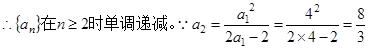
可知,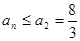
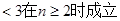 .
……14分
.
……14分

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 ,其中
,其中
 判断
判断 在
在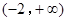 上的单调性.
上的单调性. ,
, ,当
,当 时,
时,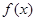 取得极值。
取得极值。 的值;
的值; 时,函数
时,函数 的图象有三个公共点,求
的图象有三个公共点,求 的取值范围。
的取值范围。