题目内容
已知集合 ,
, ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
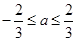 .
.
解析试题分析:解一元二次不等式 ,可得
,可得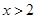 或
或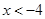 ,故
,故 或
或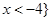 ,
,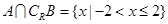 ,解一元二次不等式
,解一元二次不等式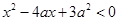 ,可得当
,可得当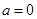 时,
时,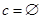 显然符合要求,当
显然符合要求,当 时,
时,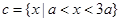 ,当
,当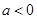 时,
时,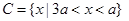 ,后两种情况均可根据
,后两种情况均可根据 建立关于
建立关于 的不等式组,从而求得
的不等式组,从而求得 的取值范围..
的取值范围..
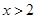 或
或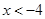 ,∴
,∴ 或
或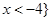 ,∴
,∴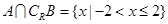 ,
,
又∵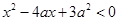 可化为
可化为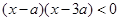 ,
,
当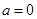 时,
时,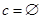 符合要求,
符合要求,
当 时,
时,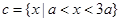 ,由
,由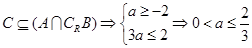 ,
,
当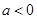 时,
时,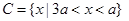 ,由
,由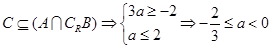 ,
,
综上, 的取值范围:
的取值范围: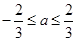 .
.
考点:1.集合的关系;2.集合的运算;3.一元二次不等式.

练习册系列答案
相关题目
 },B="{x"
},B="{x" 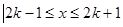 },且A
},且A B,则实数k的取值范围是
B,则实数k的取值范围是  },B={x|x2﹣5x﹣6<0,
},B={x|x2﹣5x﹣6<0,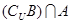 .
.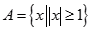 ,函数
,函数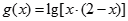 的定义域为
的定义域为 .
.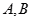 .
.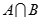 .
.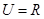 ,集合
,集合
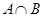 (2)求
(2)求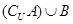
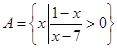 ,
,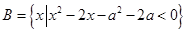
 时,求
时,求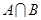 ;
;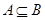 ,求实数
,求实数 的取值范围.
的取值范围.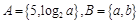 ,若
,若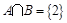 ,(1)求
,(1)求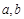 的值; (2)求
的值; (2)求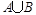 .
.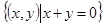 ,Q=
,Q=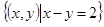 ,则A∩B=
,则A∩B= 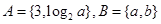 ,若
,若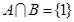 ,则
,则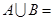 .
.