题目内容
已知集合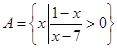 ,
,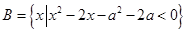
(1)当 时,求
时,求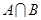 ;
;
(2)若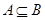 ,求实数
,求实数 的取值范围.
的取值范围.
(1)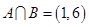 ,(2)
,(2) .
.
解析试题分析:(1)本题就是解简单分式不等式及一元二次不等式.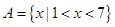 ,当
,当 时,
时, ,∴
,∴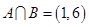 .(2)根据集合B的解集情况,讨论满足
.(2)根据集合B的解集情况,讨论满足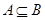 的实数
的实数 的取值范围. 因为
的取值范围. 因为 ,所以①当
,所以①当 时,
时,
 不成立;②当
不成立;②当 即
即 时,
时,
 ,解得
,解得 ③当
③当 即
即 时,
时,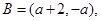
 解得
解得 综上,当
综上,当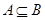 ,实数
,实数 的取值范围是
的取值范围是 .
.
法一:
解:(1)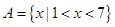 ,------2分
,------2分
当 时,
时,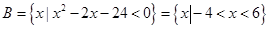 ,------4分
,------4分
∴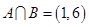 . ------6分
. ------6分
(2) ,------7分
,------7分
①当 时,
时,
 不成立;------9分
不成立;------9分
②当 即
即 时,
时,
 ,解得
,解得 ------11分
------11分
③当 即
即 时,
时,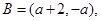
 解得
解得 ------13分
------13分
综上,当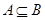 ,实数
,实数 的取值范围是
的取值范围是 .------14分(缺等号扣2分)
.------14分(缺等号扣2分)
法二:
解:(1)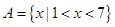 ,------2分
,------2分
当 时,
时,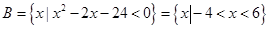 ,------4分
,------4分
∴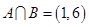 . ------6分
. ------6分
(2)记
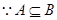
 即:
即: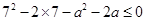 ------10分
------10分
整理得: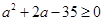 解得
解得
 实数
实数 的取值范围是
的取值范围是 .------14分(缺等号扣2分)
.------14分(缺等号扣2分)
考点:解不等式

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 ,
, ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.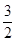 x+1,x∈[
x+1,x∈[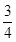 ,2]},B={x|x+m2≥1};命题p:x∈A,命题q:x∈B,并且命题p是命题q的充分条件,求实数m的取值范围.
,2]},B={x|x+m2≥1};命题p:x∈A,命题q:x∈B,并且命题p是命题q的充分条件,求实数m的取值范围.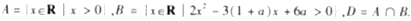
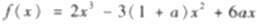 在D内的极值点.
在D内的极值点. ,
, .
. 和
和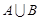 ;
;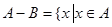 且
且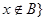 ,求
,求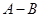 和
和 .
. 的二次方程
的二次方程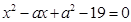 和
和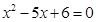 的解集分别是集合
的解集分别是集合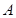 和
和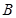 ,若
,若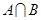 为单元素集,求
为单元素集,求 的值.
的值. 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 ,已知
,已知 :
: ;
; :
: 满足
满足 ,且若
,且若 的取值范围.
的取值范围. ,且
,且 ,则
,则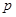 的取值范围是_________。
的取值范围是_________。 B,求实数a的取值范围.
B,求实数a的取值范围.