题目内容
如图,在三棱锥A-BCD中,AB⊥面BCD,AB=12,BC=3,CD=4,BD=5,它的正(主)视图和俯视图及有关长度如下所示:
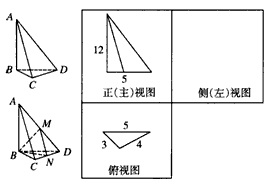
(1)在上面的方框内作出侧(左)视图,并标明最小的边长的长度;
(2)求证:在该三棱锥的表面上存在一点P,使PA=PB=PC=PD;并指出点P的位置;
(3)若M,N分别为AD,CD的中点,求四棱锥B-ACNM的体积。
(2)求证:在该三棱锥的表面上存在一点P,使PA=PB=PC=PD;并指出点P的位置;
(3)若M,N分别为AD,CD的中点,求四棱锥B-ACNM的体积。
解:(1)如图所示:
 ;
;
(2)证明:∵AB⊥面BCD,
∴AB⊥BD,AB⊥CD,
又∵BC=3,CD=4,BD=5,
∴BC⊥CD,
∴CD⊥面ABC,
∴CD⊥AC,
因此△ABD和△ACD都是以AD为斜边的直角三角形,
从而当P取AD的中点时,满足:PA=PB=PC=PD。
(3)取BD的中点D,连接MO,则MO∥AB,
从而MO⊥面BCD,且MO=6
因此 ,
,
从而, 。
。
 ;
;(2)证明:∵AB⊥面BCD,
∴AB⊥BD,AB⊥CD,
又∵BC=3,CD=4,BD=5,
∴BC⊥CD,
∴CD⊥面ABC,
∴CD⊥AC,
因此△ABD和△ACD都是以AD为斜边的直角三角形,
从而当P取AD的中点时,满足:PA=PB=PC=PD。
(3)取BD的中点D,连接MO,则MO∥AB,
从而MO⊥面BCD,且MO=6
因此
 ,
, 从而,
 。
。
练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
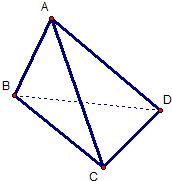 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=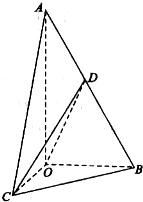 如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4, 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,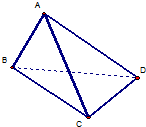 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=