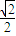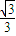题目内容
过椭圆 +
+ =1(a>b>0)的焦点垂直于x轴的弦长为
=1(a>b>0)的焦点垂直于x轴的弦长为 a,则双曲线
a,则双曲线 -
- =1的离心率e的值是
=1的离心率e的值是
- A.

- B.

- C.

- D.

B
分析:依题意,利用椭圆的通经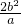 =
= a,可求得
a,可求得 =
= ,从而可求得双曲线
,从而可求得双曲线 -
- =1的离心率e的值.
=1的离心率e的值.
解答:据题意知,椭圆通径长为 a,
a,
故有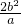 =
= a?a2=4b2?
a?a2=4b2? =
= ,
,
故相应双曲线的离心率e=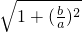 =
=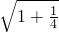 =
= .
.
故选B.
点评:本题考查椭圆与双曲线的简单性质,考查转化思想与运算能力,属于中档题.
分析:依题意,利用椭圆的通经
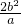 =
= a,可求得
a,可求得 =
= ,从而可求得双曲线
,从而可求得双曲线 -
- =1的离心率e的值.
=1的离心率e的值.解答:据题意知,椭圆通径长为
 a,
a,故有
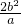 =
= a?a2=4b2?
a?a2=4b2? =
= ,
,故相应双曲线的离心率e=
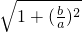 =
=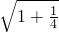 =
= .
.故选B.
点评:本题考查椭圆与双曲线的简单性质,考查转化思想与运算能力,属于中档题.

练习册系列答案
相关题目
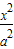 +
+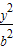 =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )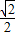
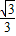


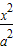 +
+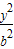 =1(a>b>0)的右焦点的弦为直径的圆与其右准线的位置关系是( )
=1(a>b>0)的右焦点的弦为直径的圆与其右准线的位置关系是( )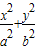 =1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB;若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB;若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.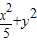 =1的“左特征点”M的坐标.
=1的“左特征点”M的坐标.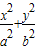 =1(a>b>0)的“左特征点”M是一个怎么样的点?并证明你的结论.
=1(a>b>0)的“左特征点”M是一个怎么样的点?并证明你的结论.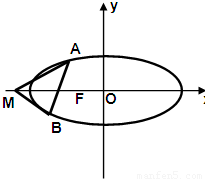
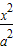 +
+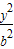 =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )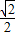
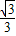


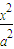 +
+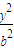 =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )