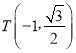题目内容
【题目】设![]() 为实数,函数
为实数,函数![]() ,
,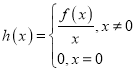
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,试判断函数
时,试判断函数![]() 在
在![]() 上的单调性,并证明.
上的单调性,并证明.
【答案】(1)![]() (2)
(2)![]() 在
在![]() 上是单调递增函数,证明见解析
上是单调递增函数,证明见解析
【解析】
(1)令x=1代入后对m的值进行讨论即可.
(2)先写出函数h(x)的解析式,然后用增函数的定义法证明.
(1)f(1)=2+(1﹣m)|1﹣m|≥4
当m>1时,(1﹣m)(m﹣1)≥2,无解;
当m≤1时,(1﹣m)(1﹣m)≥2,解得m≤1![]() .
.
所以m≤1![]() .
.
(2)由于m>0,x≥m.
所以h(x)=3x![]() 2m.
2m.
任取m≤x1≤x2,h(x2)﹣h(x1)=(x2﹣x1)(![]() )
)
x2﹣x1>0,3x1x2﹣m2>3m2﹣m2>0,x1x2>0
所以h(x2)﹣h(x1)>0即:h(x)在[m,+∞)为单调递增函数.

 名校课堂系列答案
名校课堂系列答案【题目】新高考![]() 最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
最大的特点就是取消文理分科,除语文、数学、外语之外,从物理、化学、生物、政治、历史、地理这6科中自由选择三门科目作为选考科目.某研究机构为了了解学生对全文(选择政治、历史、地理)的选择是否与性别有关,从某学校高一年级的1000名学生中随机抽取男生,女生各25人进行模拟选科.经统计,选择全文的人数比不选全文的人数少10人.
(1)估计在男生中,选择全文的概率.
(2)请完成下面的![]() 列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
列联表;并估计有多大把握认为选择全文与性别有关,并说明理由;
选择全文 | 不选择全文 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
附: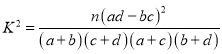 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000t生活垃圾.经分拣以后数据统计如下表(单位:![]() ):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
):根据样本估计本市生活垃圾投放情况,下列说法错误的是( )
厨余垃圾”箱 | 可回收物”箱 | 其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
A.厨余垃圾投放正确的概率为![]()
B.居民生活垃圾投放错误的概率为![]()
C.该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱
D.厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差为20000