题目内容
(本题12分)
已知椭圆 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆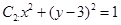 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切.
(Ⅰ)求椭圆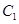 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.
【答案】
(Ⅰ) 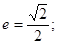 (Ⅱ)
(Ⅱ)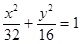 。
。
【解析】
试题分析:(Ⅰ)由题意可知直线l的方程为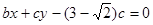 ,
,
因为直线与圆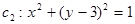 相切,所以
相切,所以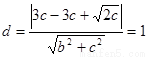 ,即
,即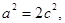
从而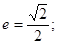 …………………5分
…………………5分
(Ⅱ)设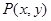 、圆
、圆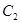 的圆心记为
的圆心记为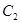 ,则
,则
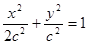 (
(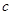 ﹥0),又
﹥0),又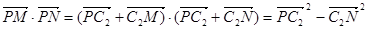 =
=
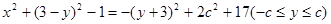 . …………………8分
. …………………8分
j当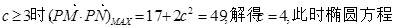
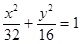 ;
;
k当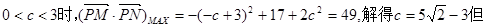
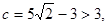 故舍去.
故舍去.
综上所述,椭圆的方程为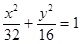 . …………………12分
. …………………12分
考点:椭圆的标准方程及简单性质;直线与圆的位置关系;直线方程的截距式;平面向量的数量积;点到直线的距离公式。
点评:本题主要考查直线、圆、椭圆的基本性质及位置关系的应用,渗透向量、函数最值等问题,培养学生综合运用知识的能力.

练习册系列答案
相关题目
 的图像关于原点对称,并且当
的图像关于原点对称,并且当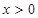 时,
时, ,试求
,试求 上的表达式,并画出它的图像,根据图像写出它的单调区间。
上的表达式,并画出它的图像,根据图像写出它的单调区间。 (1)求
(1)求 的定义域;(2)求
的定义域;(2)求
 关于点
关于点 对称.
对称. 的值.
的值. .
. 时,求函数
时,求函数 的单调递减区间;
的单调递减区间; 时,
时, 上恒大于0,求实数
上恒大于0,求实数 的取值范围.
的取值范围. 的不等式
的不等式 ,其中
,其中 .
. 变化时,试求不等式的解集
变化时,试求不等式的解集 ;
;  (其中
(其中 为整数集). 试探究集合
为整数集). 试探究集合 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合