题目内容
(本题满分14分)
已知函数 (
( ),
), .
.
(Ⅰ)当 时,解关于
时,解关于 的不等式:
的不等式: ;
;
(Ⅱ)当 时,记
时,记 ,过点
,过点 是否存在函数
是否存在函数 图象的切线?若存在,有多少条?若不存在,说明理由;
图象的切线?若存在,有多少条?若不存在,说明理由;
(Ⅲ)若 是使
是使 恒成立的最小值,对任意
恒成立的最小值,对任意 ,
,
试比较 与
与 的大小(常数
的大小(常数 ).
).
【答案】
(I) 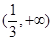 . (Ⅱ)这样的切线存在,且只有一条。
. (Ⅱ)这样的切线存在,且只有一条。
(Ⅲ)以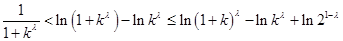 ,
,
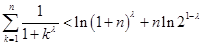 =
=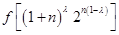 .
.
【解析】本试题主要是考查了导数在研究函数中的运用,以及不等式的求解,以及最值的研究。
(1)因为当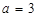 时,不等式等价于
时,不等式等价于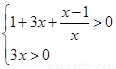 ,进而得到解集
,进而得到解集
(2)假设存在这样的切线,设其中一个切点 ,
,
∴切线方程: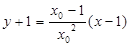 将点T代入得到结论。
将点T代入得到结论。
(3)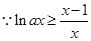 对
对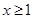 恒成立,所以
恒成立,所以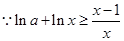
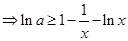 ,构造函数运用导数求解最值得到证明。
,构造函数运用导数求解最值得到证明。
(I)当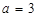 时,不等式等价于
时,不等式等价于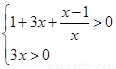 ,解集为
,解集为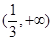 .
3分
.
3分
(Ⅱ)假设存在这样的切线,设其中一个切点 ,
,
∴切线方程: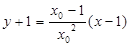 ,将点
,将点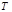 坐标代入得:
坐标代入得:
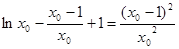 ,即
,即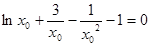 ,
①
,
①
法1:设 ,则
,则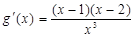 .………………6分
.………………6分
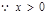 ,
,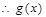 在区间
在区间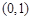 ,
,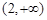 上是增函数,在区间
上是增函数,在区间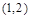 上是减函数,
上是减函数,
故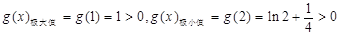 .
.
又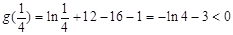 ,注意到
,注意到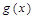 在其定义域上的单调性知
在其定义域上的单调性知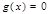 仅在
仅在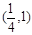 内有且仅有一根方程①有且仅有一解,故符合条件的切线有且仅有一条. 8分.
内有且仅有一根方程①有且仅有一解,故符合条件的切线有且仅有一条. 8分.
法2:令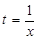 (
( ),考查
),考查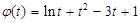 ,则
,则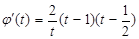
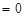 ,
,
从而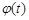 在
在 增,
增, 减,
减,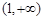 增. 故
增. 故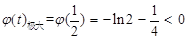 ,
,
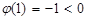 ,而
,而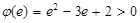 ,故
,故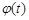 在
在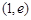 上有唯一解.
上有唯一解.
从而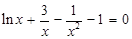 有唯一解,即切线唯一.
有唯一解,即切线唯一.
法3: ,
,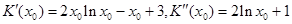 ;
;
当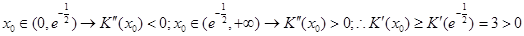 ;
;
所以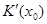 在
在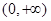 单调递增。
又因为
单调递增。
又因为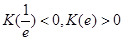 ,所以方程
,所以方程
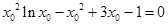 有必有一解,所以这样的切线存在,且只有一条。
有必有一解,所以这样的切线存在,且只有一条。
(Ⅲ)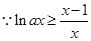 对
对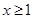 恒成立,所以
恒成立,所以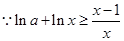
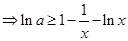 ,
,
令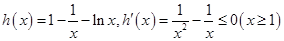 ,可得
,可得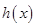 在区间
在区间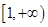 上单调递减,
上单调递减,
故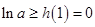 ,
,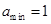 .
10分
.
10分
得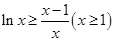 ,
,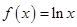 . 令
. 令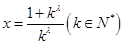 ,
,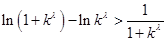 ,
,
注意到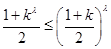 ,即
,即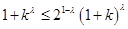 ,
,
所以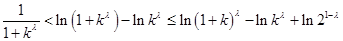 ,
,
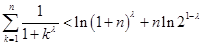 =
=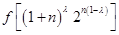 .
14分
.
14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 B=[0,3],求实数m的值
B=[0,3],求实数m的值 CRB,求实数m的取值范围
CRB,求实数m的取值范围 是⊙
是⊙ :
: 上的任意一点,过
上的任意一点,过 垂直
垂直 轴于
轴于 ,动点
,动点 满足
满足 。
。 ,在动点
,在动点 、
、 ,使
,使 (O是坐标原点),若存在,求出直线
(O是坐标原点),若存在,求出直线 的方程,若不存在,请说明理由。
的方程,若不存在,请说明理由。 .
. 的定义域;
的定义域; 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使
 ).
).