题目内容
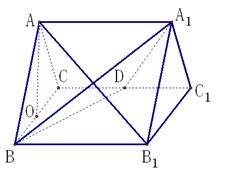
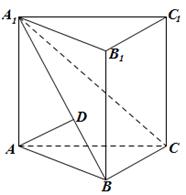
如图,三棱柱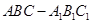 的所有棱长都为
的所有棱长都为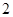 ,且
,且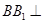 平面
平面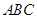 ,
,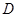 为
为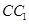 中点.
中点.
(Ⅰ)求证: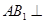 面
面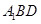 ;
;
(Ⅱ)求二面角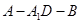 的大小的余弦值;
的大小的余弦值;
(Ⅲ)求点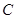 到平面
到平面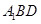 的距离.
的距离.
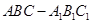 的所有棱长都为
的所有棱长都为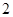 ,且
,且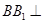 平面
平面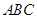 ,
,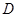 为
为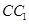 中点.
中点.
(Ⅰ)求证:
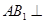 面
面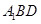 ;
;(Ⅱ)求二面角
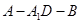 的大小的余弦值;
的大小的余弦值;(Ⅲ)求点
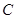 到平面
到平面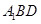 的距离.
的距离.(1)欲证AB1⊥平面A1BD,根据直线与平面垂直的判定定理可知只需证AB1与平面A1BD内两相交直线垂直,而AB1⊥A1B,AB1⊥DO,A1B∩DO=O,满足定理所需条件.
(2)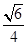
(3)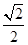
(2)
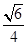
(3)
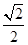
试题分析:解析: (Ⅰ)取
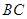 中点
中点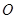 ,连结
,连结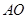 .
.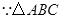 为正三角形,
为正三角形,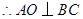 .
.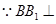 平面
平面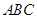 ,
,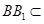 平面
平面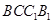
 平面
平面 平面
平面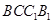 ,
,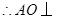 平面
平面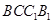 . 1分
. 1分取
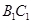 中点
中点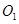 ,以
,以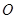 为原点,
为原点,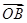 ,
,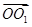 ,
,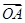 的方向为
的方向为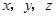 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则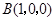 ,
,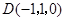 ,
,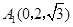 ,
,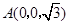 ,
,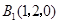 ,
,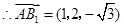 ,
,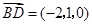 ,
,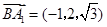 .
.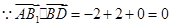 ,
,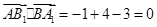 ,
,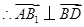 ,
,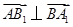 ,
,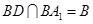 .
.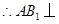 平面
平面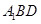 . 4分
. 4分(Ⅱ)设平面
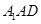 的法向量为
的法向量为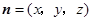 .
.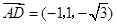 ,
,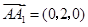 .
.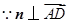 ,
,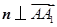 ,
,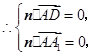
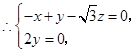
取
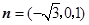 为平面
为平面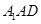 的一个法向量.
的一个法向量.由(Ⅰ)知
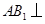 平面
平面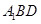 ,
,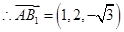 为平面
为平面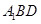 的法向量.
的法向量.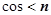 ,
,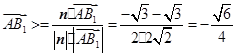 .
.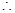 二面角
二面角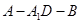 的余弦值为
的余弦值为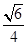 . 9分
. 9分(Ⅲ)由(Ⅱ),
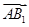 为平面
为平面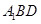 法向量,
法向量,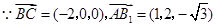 .
.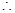 点
点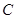 到平面
到平面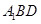 的距离
的距离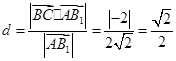 . 13分
. 13分点评:主要是考查了运用向量法来求解空间中的角和距离的求解,属于中档题。

练习册系列答案
相关题目
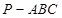 中,
中,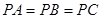 ,底面
,底面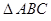 是正三角形,
是正三角形,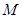 、
、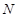 分别是侧棱
分别是侧棱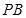 、
、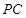 的中点.若平面
的中点.若平面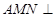 平面
平面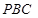 ,则平面
,则平面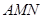 与平面
与平面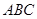 所成二面角(锐角)的余弦值等于( )
所成二面角(锐角)的余弦值等于( )




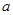 的正方体
的正方体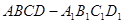 中,错误的是( )
中,错误的是( )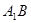 和直线
和直线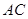 所成角的大小为
所成角的大小为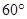
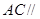 平面
平面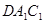
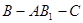 的大小是
的大小是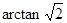
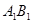 到平面
到平面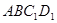 的距离为
的距离为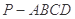 中,底面
中,底面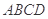 为正方形,
为正方形,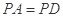
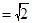 ,
,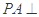 平面
平面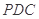 ,
,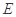 为棱
为棱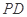 的中点.
的中点.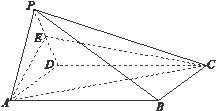
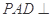 平面
平面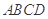 ;
; 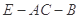 的余弦值.
的余弦值.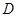 到平面
到平面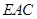 的距离.
的距离.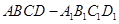 中,已知
中,已知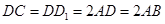 ,
,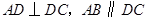 .
.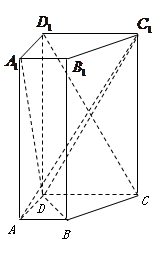
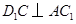 ;
;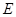 是
是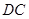 上一点,试确定
上一点,试确定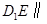 平面
平面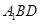 ,并说明理由.
,并说明理由.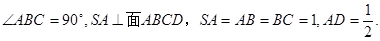
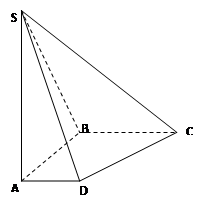
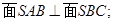
 ,AB=BC=2,P为AC中点,求三棱锥
,AB=BC=2,P为AC中点,求三棱锥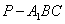 的体积。
的体积。