题目内容
设A，B为x轴上两点，点M的横坐标为2，且(
+
)⊥
，若直线MA的方程为x-y+1=0，则直线MB的方程为（ ）
| MA |
| MB |
| AB |
分析：根据B点既在x轴上，又在直线x-y+1=0上，先求出B点坐标，然后根据M点既在直线x-y+1=0上，又给出了横坐标求出点M的坐标，再由(
+
)⊥
，说明M在AB的垂直平分线上，根据对称性求得A，运用两点式写MB的方程．
| MA |
| MB |
| AB |
解答：解：在方程为x-y+1=0中，取y=0，得x=-1，所以得B点的坐标为（-1，0），
又因为点M的横坐标为2，所以M在直线x=2
上，联立
得
，所以点M（2，3），
因为(
+
)⊥
，知道M在AB的中垂线上，由对称性知A（5，0），
由两点式可得直线MB的方程为x+y-5=0．
故选D．
又因为点M的横坐标为2，所以M在直线x=2
上，联立
|
|
因为(
| MA |
| MB |
| AB |
由两点式可得直线MB的方程为x+y-5=0．
故选D．
点评：本题考查了运用数量积判断两个平面向量的垂直关系，考查了数形结合思想，解答此题的关键是由(
+
)⊥
，说明M在AB的中垂线上，考查了学生综合解题能力．
| MA |
| MB |
| AB |
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
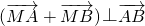，若直线MA的方程为x-y+1=0，则直线MB的方程为
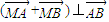，若直线MA的方程为x-y+1=0，则直线MB的方程为（ ）