Question

（2012•蓝山县模拟）设A、B为x轴上两点，点P的横坐标为2，且|PA|=|PB|，若直线PA的方程为x-2y+1=0，则直线PB的方程是

x+2y-5=0

．

Answer 1

分析：把P点的横坐标代入x-2y+1=0求出纵坐标得到P的坐标，然后根据|PA|=|PB|得到P在线段AB的垂直平分线上，则过P作PQ⊥x轴即为AB的中垂线，根据中点坐标公式求出点B的坐标，然后根据P和B的坐标写出直线方程即可．

解答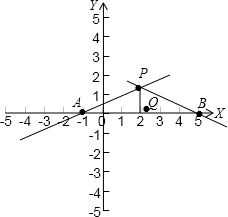：解：根据|PA|=|PB|得到点P一定在线段AB的垂直平分线上，
根据x-2y+1=0求出点A的坐标为（-1，0），由P的横坐标是2代入x-2y+1=0求得纵坐标为

3

2

，则P（2，

3

2

），
又因为Q为A与B的中点，所以得到B（5，0），所以直线PB的方程为：y-0=

3 2 -0

2-5

（x-5）化简后为x+2y-5=0
故答案为：x+2y-5=0．

点评：此题是一道基础题，要求学生会根据题中的条件利用数形结合的数学思想解决实际问题．考查学生会根据两点坐标写出直线的一般式方程．