��Ŀ����
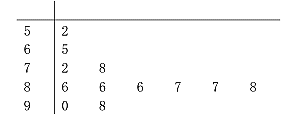
����Ŀ����֪�����з��д�С����״��ͬ��С�����ɣ����б��Ϊ0��С��1�������Ϊ1��С��1�������Ϊ2��С��![]() ��.���Ӵ����������ȡ1��С��ȡ�����Ϊ2��С��ĸ�����
��.���Ӵ����������ȡ1��С��ȡ�����Ϊ2��С��ĸ�����![]() .
.
��1����![]() ��ֵ��
��ֵ��
��2���Ӵ����в��Żص������ȡ2��С�ǵ�һ��ȡ����С����Ϊ![]() ���ڶ���ȡ����С����Ϊ
���ڶ���ȡ����С����Ϊ![]() .
.
�ټ���![]() ��Ϊ�¼�
��Ϊ�¼�![]() �����¼�
�����¼�![]() �ĸ��ʣ�
�ĸ��ʣ�
��������![]() ����ȡ2��ʵ��
����ȡ2��ʵ��![]() ��
��![]() �����¼���
�����¼���![]() ��������ĸ���.
��������ĸ���.
���𰸡���1��2����2����![]() ����
����![]()
��������
��1���ȸ��ݹŵ����ʽ�дӴ����������ȡ1��С��ȡ�����Ϊ2��С��ĸ��ʣ���ý����
��2������ȷ�����Żص������ȡ2������ȷ�������¼�������ȷ����![]() �������������¼����������ݹŵ������������
�������������¼����������ݹŵ������������
���ȸ��ݺ��������![]() ���ٸ��ݼ��θ��ͣ�����ͣ����ʹ�ʽ����.
���ٸ��ݼ��θ��ͣ�����ͣ����ʹ�ʽ����.
��1�����ݴӴ��������ȡ1��С��ȡ�����Ϊ2��С��ĸ�����![]() ���ɵ�
���ɵ�![]() .
.
���![]() .
.
��2���ٴӴ����в��Żص������ȡ2�����л����¼�12����������![]() ��Ϊ�¼�
��Ϊ�¼�![]() �Ļ����¼���4������
�Ļ����¼���4������![]() .
.
����![]() �������Ϊ�¼�
�������Ϊ�¼�![]() �����¼�
�����¼�![]() �ȼ�����
�ȼ�����![]() ���������
���������![]() ���Կ���ƽ���еĵ㣬��ȫ����������ɵ�����Ϊ
���Կ���ƽ���еĵ㣬��ȫ����������ɵ�����Ϊ![]() ����������ȵõ��¼�
����������ȵõ��¼�![]() .
.

��ϰ��ϵ�д�
�����Ŀ