题目内容
已知平面向量| α |
| β |
| α |
| β |
| β |
| α |
| α |
| β |
| α |
| β |
| β |
| β |
| α |
| β |
| β |
分析:(1)由|
-
|=|
+
|=2即|
-
|2=|
+
|2=4,化简得
可求
(2)可设
=
,
=
,则
=
-
,由题可得在△ABO中,∠OBA=60°,由正弦定理,
=
,
可得|
|=
sinA,由0°<A<120° 可求
| α |
| β |
| α |
| β |
| α |
| β |
| α |
| β |
|
(2)可设
| OA |
| α |
| OB |
| β |
| BA |
| α |
| β |
|
| ||
| sinA |
|
| ||
| sinB |
可得|
| β |
2
| ||
| 3 |
解答: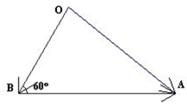 解:(1)|
解:(1)|
-
|=|
+
|=2即|
-
|2=|
+
|2=4,化简得
∵|
|=1,∴|
|=
,即|
|的值为
(2)如图,设
=
,
=
,∴
=
-
,
由题,
与
-
的夹角为120°,因此,在△ABO中,∠OBA=60°,根据正弦定理,
=
,
∴|
|=
sinA,∵0°<A<120°∴0<sinA≤1,
即|
|的取值范围是(0,
].
 解:(1)|
解:(1)|| α |
| β |
| α |
| β |
| α |
| β |
| α |
| β |
|
∵|
| α |
| β |
| 3 |
| β |
| 3 |
(2)如图,设
| OA |
| α |
| OB |
| β |
| BA |
| α |
| β |
由题,
| β |
| α |
| β |
|
| ||
| sinA |
|
| ||
| sinB |
∴|
| β |
2
| ||
| 3 |
即|
| β |
2
| ||
| 3 |
点评:本题主要考查了平面向量的数量积性质,三角形的正弦定理的应用,三角函数的性质的综合应用,属于基础知识的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知平面向量
=(1,-3),
=(4,-2),λ
+
与
垂直,则λ是( )
| a |
| b |
| a |
| b |
| a |
| A、-1 | B、1 | C、-2 | D、2 |
已知平面向量
,
满足|
|=1,|
|=2,
与
的夹角为60°,则“m=1”是“(
-m
)⊥
”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |