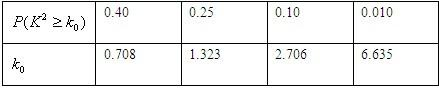
题目内容
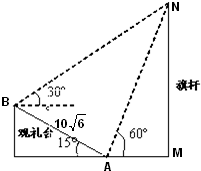2010年11月12日广州亚运会上举行升旗仪式．如图，在坡度为15°的观礼台上，某一列座位所在直线AB与旗杆所在直线MN共面，在该列的第一个座位A和最后一个座位B测得旗杆顶端N的仰角分别为60°和30°，且座位A、B的距离为10| 6 |
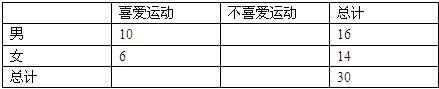
30
30
米．分析：先画出示意图，根据题意可求得∠NBA和∠BAN，则∠BNA可求，然后利用正弦定理求得AN，最后在Rt△AMN中利用MN=AN•sin∠NAM求得答案．
解答：解：如图所示，依题意可知∠NBA=45°，
∠BAN=180°-60°-15°=105°
∴∠BNA=180°-45°-105°=30°
由正弦定理可知 CEsin∠EAC=ACsin∠CEA，
=
∴AN=
• sin∠NBA=20
米
∴在Rt△AMN中，
MN=AN•sin∠NAM=20
×
=30米
所以：旗杆的高度为30米
故答案为：30．
∠BAN=180°-60°-15°=105°
∴∠BNA=180°-45°-105°=30°
由正弦定理可知 CEsin∠EAC=ACsin∠CEA，
| AB |
| sin∠BNA |
| NA |
| sin∠NBA |
∴AN=
| AB |
| sin∠BNA |
| 3 |
∴在Rt△AMN中，
MN=AN•sin∠NAM=20
| 3 |
| ||
| 2 |
所以：旗杆的高度为30米
故答案为：30．
点评：本题主要考查了解三角形的实际应用．此类问题的解决关键是建立数学模型，把实际问题转化成数学问题，利用所学知识解决．
练习册系列答案
相关题目
