题目内容
13.设函数f(x)=(2x+a)n,其中n=6${∫}_{0}^{\frac{π}{2}}$cosxdx,$\frac{f′(0)}{f(0)}$=-12,则f(x)的展开式中x4的系数是( )| A. | -240 | B. | 240 | C. | -60 | D. | 60 |
分析 利用定积分基本定理可求得n,利用$\frac{f′(0)}{f(0)}$=-12,求出a,再利用二项式定理可求得f(x)展开式中x4的系数.
解答 解:∵n=6${∫}_{0}^{\frac{π}{2}}$cosxdx=6sinx${|}_{0}^{\frac{π}{2}}$=6,
∴f(x)=(2x+a)6,
∴f(0)=a6,f′(0)=12a5,
∵$\frac{f′(0)}{f(0)}$=-12,
∴a=-1
∴f(x)=(2x-1)6展开式中x4的系数为:${C}_{6}^{2}$•24•(-1)2=15×16=240.
故选:B.
点评 本题考查二项式定理,考查定积分,求得n是关键,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
4.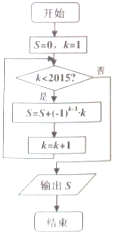 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )
 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )| A. | -1008 | B. | -1007 | C. | 1007 | D. | 1008 |
2.已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=lnx+x,若f(a)=g(b)=h(c)=0,则( )
| A. | c<b<a | B. | b<c<a | C. | a<b<c | D. | a<c<b |