题目内容
20.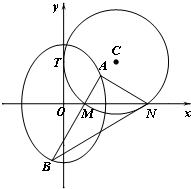 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3.(Ⅰ)求圆C的方程;
(Ⅱ)过点M任作一条直线与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{8}$=1相交于两点A、B,连接AN、BN,求证:∠ANM=∠BNM.
分析 (Ⅰ)设圆的半径为r吗,根据|MN|=3求出r,即可确定出圆C的方程;
(Ⅱ) 把y=0代入圆方程求出x的值,确定出M与N坐标,当AB⊥x轴时,由椭圆的对称性得证;当AB与x轴不垂直时,设直线AB解析式为y-k(x-1),与椭圆方程联立消去y得到关于x的一元二次方程,设直线AB交椭圆于A(x1,y1),B(x2,y2),利用韦达定理表示出x1+x2,x1x2,进而表示出直线AN与直线BN斜率之和为0,即可得证.
解答 解:(Ⅰ)设圆C的半径为r(r>0),
依题意,圆心坐标为(r,2),
∵|MN|=3,
∴r2=($\frac{3}{2}$)2+22=$\frac{25}{4}$,
∴圆C的方程为(x-$\frac{5}{2}$)2+(y-2)2=$\frac{25}{4}$;
(Ⅱ)把y=0代入方程(x-$\frac{5}{2}$)2+(y-2)2=$\frac{25}{4}$,
解得:x=1,或x=4,即M(1,0),N(4,0),
当AB⊥x轴时,由椭圆的对称性可知∠ANM=∠BNM;
当AB与x轴不垂直时,设直线AB解析式为y=k(x-1),
联立方程$\left\{\begin{array}{l}{y=k(x-1)}\\{2{x}^{2}+{y}^{2}=8}\end{array}\right.$,
消去y得:(k2+2)x2-2k2x+k2-8=0,
设直线AB交椭圆于A(x1,y1),B(x2,y2),
则有x1+x2=$\frac{2{k}^{2}}{{k}^{2}+2}$,x1x2=$\frac{{k}^{2}-8}{{k}^{2}+2}$,
∵y1=k(x1-1),y2=k(x2-1),
∴kAN+kBN=$\frac{{y}_{1}}{{x}_{1}-4}$+$\frac{{y}_{2}}{{x}_{2}-4}$=$\frac{k({x}_{1}-1)}{{x}_{1}-4}$+$\frac{k({x}_{2}-1)}{{x}_{2}-4}$=$\frac{k({x}_{1}-1)({x}_{1}-4)+k({x}_{2}-1)({x}_{2}-4)}{({x}_{1}-1)({x}_{2}-4)}$,
∵(x1-1)(x2-4)+(x2-1)(x1-4)=2x1x2-5(x1+x2)+8=$\frac{2({k}^{2}-8)}{{k}^{2}+2}$-$\frac{10{k}^{2}}{{k}^{2}+2}$+8=0,
∴kAN+kBN=0,∠ANM=∠BNM,
综上所述,∠ANM=∠BNM.
点评 此题考查了直线与圆方程的应用,椭圆的简单性质,圆的标准方程,熟练掌握运算法则是解本题的关键.

 小学课时特训系列答案
小学课时特训系列答案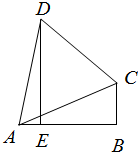 如图,在△ABC中,∠B为直角,DE⊥AB于E,AC⊥DC,设BC=1.
如图,在△ABC中,∠B为直角,DE⊥AB于E,AC⊥DC,设BC=1.