题目内容
1．化简$（\overrightarrow{AB}-\overrightarrow{BM}）+（\overrightarrow{BD}+\overrightarrow{BC}）+\overrightarrow{DM}$的结果是$\overrightarrow{AC}$．分析 利用向量的三角形法则与多边形法则即可得出．
解答 解：原式=$（\overrightarrow{AB}+\overrightarrow{BD}）$+$\overrightarrow{BC}$+$（\overrightarrow{DM}+\overrightarrow{MB}）$
=$\overrightarrow{AD}+\overrightarrow{DB}$+$\overrightarrow{BC}$
=$\overrightarrow{AC}$．
故答案为：$\overrightarrow{AC}$．
点评 本题考查了向量的三角形法则与多边形法则，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
12．某学校安排3位老师与5名学生去3地参观学习，每地至少去1名老师和1名学生，则不同的安排方法总数为（ ）
| A． | 1800 | B． | 900 | C． | 300 | D． | 1440 |
6．
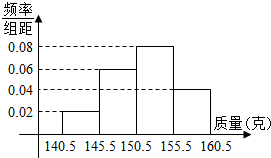为了了解某种进口茶叶的质量（单位：克），从中抽取若干包进行检查，获得样本的频率分布直方图如图所示．若已知样本中质量在[155.5，160.5）内的茶叶有10包，则样本容量为（ ）
为了了解某种进口茶叶的质量（单位：克），从中抽取若干包进行检查，获得样本的频率分布直方图如图所示．若已知样本中质量在[155.5，160.5）内的茶叶有10包，则样本容量为（ ）| A． | 150 | B． | 100 | C． | 70 | D． | 50 |
10．已知集合A={x|-1≤x＜2}，B={x|-x≥0}，则A∩B等于（ ）
| A． | {x|0≤x＜2} | B． | {x|-2＜x≤-1} | C． | {x|-2＜x≤0} | D． | {x|-1≤x≤0} |
11．${2^{\frac{3}{4}}}$化成根式形式为（ ）
| A． | $\root{3}{2^4}$ | B． | $\root{4}{3^2}$ | C． | $\root{4}{2^3}$ | D． | $\root{2}{4^3}$ |