��Ŀ����
����Ŀ��ij��˫һ��A������ѧ��ҵ���Ӹ�У2018���Ѿ�ҵ�Ĵ�ѧ���Ʊ�ҵ���������ȡ��100�˽����ʾ����飬����һ�������ǵ���н������������鷢�֣����ǵ���н�����������1.65��Ԫ��2.35��Ԫ֮�䣬����ͳ�����ݷ��飬�õ����µ�Ƶ�ʷֲ�ֱ��ͼ��

��1��Ϊ��лͬѧ�Ƕ�������鹤����֧�֣���У���÷ֲ�����ķ�����������ǰ�����г��6�ˣ�������һ����Ʒ��������6�����ٳ�ȡ2�ˣ�������ij�������ֻ�1��������������ֻ���2����н��������1.75��Ԫ�ĸ��ʣ�
��2��ͬһ�������ø�������е�ֵ������.
��i������100����н���������ƽ����![]() ����������
����������![]() ��
��
��ii����У��ij������ҵ��2018�챾�Ʊ�ҵ����50�ˣ�������2019���쳤���ڼ�ٰ�һ��ͬѧ����ᣬ����ȡһ���Ļ���ã��������շѷ�����
����һ����![]() ����н��������
����н��������![]() ����ÿ����ȡ400Ԫ����н��������
����ÿ����ȡ400Ԫ����н��������![]() �ڵ�ÿ���յ�600Ԫ����н��������
�ڵ�ÿ���յ�600Ԫ����н��������![]() �Ҳ��ÿ����ȡ800Ԫ.
�Ҳ��ÿ����ȡ800Ԫ.
����������ÿ��һ����нˮ��3%��ȡ���ø�У��ҵ��ͳ�Ƶ���100����н���������Ƶ�ʽ��й��㣬��һ���շѷ������յ�����ķ��ã�
�ο����ݣ�![]() .
.
���𰸡���1��![]() ����2����i��2��
����2����i��2��![]() ����ii������һ.
����ii������һ.
��������
��1������Ƶ�ʷֲ�ֱ��ͼ���ǰ2���е��������ɷֲ�����ó�ȡ��������Ȼ���6�˱�ţ���д����ȡ2�˵�������ϣ�Ҳ�ɵó����������ֻ���2����н��������1.75��Ԫ��������ϣ��Ӷ��ɼ�������ʣ�
��2������Ƶ�ʷֲ�ֱ��ͼ�������ֵ�ͷ��Ȼ���������![]() �����Ƶ�ʷֲ�ֱ��ͼ�ɼ������������ȡ�ķ��ã�
�����Ƶ�ʷֲ�ֱ��ͼ�ɼ������������ȡ�ķ��ã�
��1����һ����![]() �ˣ��ڶ�����
�ˣ��ڶ�����![]() ��.
��.
���շֲ������6��ʱ����һ���1�ˣ���Ϊ![]() ���ڶ����5�ˣ���Ϊ
���ڶ����5�ˣ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
����6���г�2�˹���15�֣�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
�� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
���������ֻ���2����н��������1.75��Ԫ��10�֣�![]() ��
��![]() ��
�� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
���ǻ��������ֻ���2����н������1.75��Ԫ�ĸ���![]() .
.
��2����i����100����н���������ƽ����![]() ����������
����������![]() �ֱ���
�ֱ���![]()
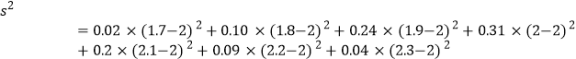
![]() ��
��
��ii������һ��
![]()
��н��������![]() ����ջ����ԼΪ
����ջ����ԼΪ![]() ����Ԫ����
����Ԫ����
��н��������![]() �ջ����ԼΪ
�ջ����ԼΪ![]() ����Ԫ����
����Ԫ����
��н��������![]() �Ҳ��ջ����ԼΪ
�Ҳ��ջ����ԼΪ![]() ����Ԫ������
����Ԫ������
��˷���һ����50�˹��ջ����ԼΪ3.01����Ԫ��.
����������50�˹��ջ����ԼΪ![]() ����Ԫ��.
����Ԫ��.
�ʷ���һ���յ�����ķ���.