题目内容
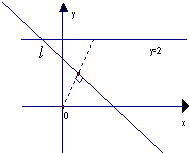 如图,在直角坐标系xoy中,坐标原点O(0,0),以动直线l:y=mx+n(m,n∈R)为轴翻折,使得每次翻折后点O都落在直线y=2上.
如图,在直角坐标系xoy中,坐标原点O(0,0),以动直线l:y=mx+n(m,n∈R)为轴翻折,使得每次翻折后点O都落在直线y=2上.(1)求以(m,n)为坐标的点的轨迹G的方程;
(2)过点E(0,
| 5 | 4 |
分析:(1)因为每次翻折后点O都落在直线y=2上.所以消参法求轨迹方程.
(2)(ⅰ)可先设出直线MN方程为y=kx+
,与(1)中所得轨迹方程联立,得到带参数k的一元二次方程,再用弦长公式求MN长,所求长度等于3,则得到关于k的方程,在解方程,即可得到k值进而求出M,N纵坐标之和.
(ⅱ)先假设存在直线,使△OMN的面积等于某一给定的正常数,再通过计算△OMN的面积,来判断假设是否正确.
(2)(ⅰ)可先设出直线MN方程为y=kx+
| 5 |
| 4 |
(ⅱ)先假设存在直线,使△OMN的面积等于某一给定的正常数,再通过计算△OMN的面积,来判断假设是否正确.
解答:解:(1)设点O翻折后的坐标为(x0,2),当x0≠0时,有
+n=1,
• m=-1,消去x0,得,
n=m2+1.
当x0=0时,得m=0,n=1.
综上,动点的轨迹方程为y=x2+1.
(2)(ⅰ)设过点E(0,
)作斜率为k的直线方程y=kx+
,M(x1,y1,),N(x2,y2),
由
得,x2-kx-
=0
x1+x2=k,x1x2=-
.
|MN|=
|x1-x2|=1+k2=3,∴k2=2.
y1+y2=k(x1+x2)+
=k2+
=
(ⅱ)O点到直线y=kx+
的距离d=
,使△OMN的面积S=
|MN|d=
≥
a>
时,存在两条直线满足条件
a=
时,存在一条直线满足条件
a<
时,不存在直线满足条件.
| mx0 |
| 2 |
| 2 |
| x0 |
n=m2+1.
当x0=0时,得m=0,n=1.
综上,动点的轨迹方程为y=x2+1.
(2)(ⅰ)设过点E(0,
| 5 |
| 4 |
| 5 |
| 4 |
由
|
| 1 |
| 4 |
x1+x2=k,x1x2=-
| 1 |
| 4 |
|MN|=
| 1+k2 |
y1+y2=k(x1+x2)+
| 5 |
| 2 |
| 5 |
| 2 |
| 9 |
| 2 |
(ⅱ)O点到直线y=kx+
| 5 |
| 4 |
| 5 | ||
4
|
| 1 |
| 2 |
| 5 |
| 8 |
| 1+k2 |
| 5 |
| 8 |
a>
| 5 |
| 8 |
a=
| 5 |
| 8 |
a<
| 5 |
| 8 |
点评:本题主要考查了消参法求轨迹方程,以及弦长公示的利用,计算量较大,须认真计算,避免出错.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 (2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.
(2009•杭州二模)如图,在直角坐标系xOy中,锐角△ABC内接于圆x2+y2=1.已知BC平行于x轴,AB所在直线方程为y=kx+m(k>0),记角A,B,C所对的边分别是a,b,c.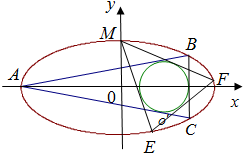 如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为
如图,在直角坐标系中,中心在原点,焦点在X轴上的椭圆G的离心率为 (2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
(2013•石景山区二模)如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且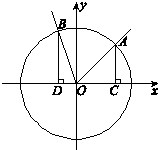 如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: