题目内容
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知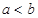 ,且
,且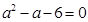 ,
,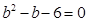 ,数列
,数列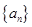 、
、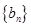 满足
满足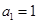 ,
,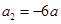 ,
, ,
,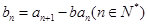 .
.
(1) 求证数列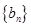 是等比数列;
是等比数列;
(2) (理科)求数列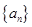 的通项公式
的通项公式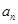 ;
;
(3) (理科)若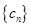 满足
满足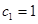 ,
,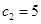 ,
,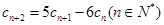 ,试用数学归纳法证明:
,试用数学归纳法证明:
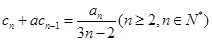 .
.
【答案】
证明(1)∵ ,
,
∴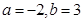 ,
,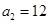 .
.
∵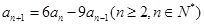 ,
,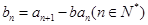 ,
,
∴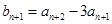
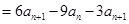
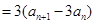
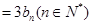 .
.
又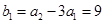 ,
,
∴数列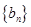 是公比为3,首项为
是公比为3,首项为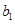 的等比数列.
的等比数列.
解(2)(理科)依据(1)可以,得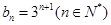 .
.
于是,有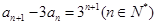 ,即
,即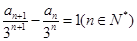 .
.
因此,数列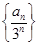 是首项为
是首项为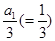 ,公差为1的等差数列.
,公差为1的等差数列.
故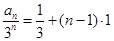 .
.
所以数列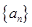 的通项公式是
的通项公式是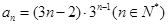 .
.
(3)(理科)用数学归纳法证明: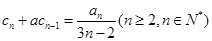
(i)当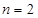 时,左边
时,左边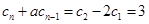 ,右边
,右边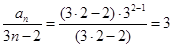 ,
,
即左边=右边,所以当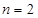 时结论成立.
时结论成立.
(ii)假设当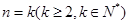 时,结论成立,即
时,结论成立,即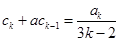 .
.
当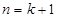 时,左边
时,左边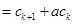
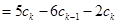
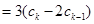
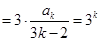 ,
,
右边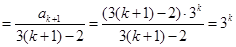 .
.
即左边=右边,因此,当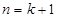 时,结论也成立.
时,结论也成立.
根据(i)、(ii)可以断定,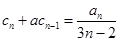 对
对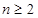 的正整数都成立.
的正整数都成立.
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处