题目内容
【题目】如图所示，在直角坐标系
中，曲线
由中心在原点，焦点在
轴上的半椭圆和以原点为圆心，半径为2的半圆构成，以坐标原点
为极点，轴正半轴为极轴建立极坐标系.
（1）写出曲线的极坐标方程；
（2）已知射线
与曲线交于点
，点
为曲线上的动点，求
面积的最大值.
【答案】（1）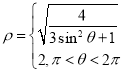
，
；（2）
.
【解析】
（1）分别写出曲线
的上、下两半部分的直角坐标方程，结合极坐标与直角坐标的互化公式，即可求解；
（2）把射线
代入曲线的极坐标方程，求得点
的极经，然后写出
的面积，求得其最大值即可.
（1）由题设可知，曲线上半部分的直角坐标方程为
，
所以，曲线上半部分的极坐标方程为
曲线下半部分的直角坐标方程为
，
所以，曲线下半部分的极坐标方程为
，
故曲线的极坐标方程为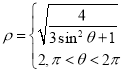
，.
（2）由题设，将代入曲线的极坐标方程可得：
，
又点
为曲线上的动点，所以
，
由面积公式得：
，
当且仅当
，
时等号成立，
故面积的最大值为.
练习册系列答案
相关题目
