题目内容
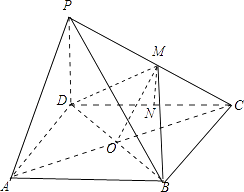
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=60°,AB=2AD,PD⊥平面ABCD,点M为PC的中点. 
(1)求证:PA∥平面BMD;
(2)求证:AD⊥PB;
(3)若AB=PD=2,求点A到平面BMD的距离.
【答案】
(1)证明:设AC和BD交于点O,则由底面ABCD是平行四边形可得O为AC的中点.
由于点M为PC的中点,故MO为三角形PAC的中位线,故MO∥PA.再由PA不在平面BMD内,而MO在平面BMD内,
故有PA∥平面BMD
(2)证明:由PD⊥平面ABCD,可得PD⊥AD,平行四边形ABCD中,∵∠BCD=60°,AB=2AD,
∴cos∠BAD= ![]() =cos60°=
=cos60°= ![]() ,∴AD⊥BD.
,∴AD⊥BD.
这样,AD垂直于平面PBD内的两条相交直线,故AD⊥平面PBD,∴AD⊥PB
(3)解:若AB=PD=2,则AD=1,BD=ABsin∠BAD=2× ![]() =
= ![]() ,
,
由于平面BMD经过AC的中点,故点A到平面BMD的距离等于点C到平面BMD的距离.
取CD得中点N,则MN⊥平面ABCD,且MN= ![]() PD=1.
PD=1.
设点C到平面MBD的距离为h,则h为所求.
由AD⊥PB 可得BC⊥PB,故三角形PBC为直角三角形.
由于点M为PC的中点,利用直角三角形斜边的中线等于斜边的一半,可得MD=MB,故三角形MBD为等腰三角形,
故MO⊥BD.
由于PA= ![]() =
= ![]() =
= ![]() ,∴MO=
,∴MO= ![]() .
.
由VM﹣BCD=VC﹣MBD 可得, ![]() (
( ![]() )MN=
)MN= ![]() (
( ![]() ×BD×MO )×h,
×BD×MO )×h,
故有 ![]() ×(
×( ![]() )×1=
)×1= ![]() (
( ![]() )h,
)h,
解得h= ![]() .
.
【解析】(1)设AC和BD交于点O,MO为三角形PAC的中位线可得MO∥PA,再利用直线和平面平行的判定定理,证得结论.(2)由PD⊥平面ABCD,可得PD⊥AD,再由cos∠BAD= ![]() =
= ![]() ,证得 AD⊥BD,可证AD⊥平面PBD,从而证得结论.(3)点A到平面BMD的距离等于点C到平面BMD的距离h,求出MN、MO的值,利用等体积法求得点C到平面MBD的距离h.
,证得 AD⊥BD,可证AD⊥平面PBD,从而证得结论.(3)点A到平面BMD的距离等于点C到平面BMD的距离h,求出MN、MO的值,利用等体积法求得点C到平面MBD的距离h.
【考点精析】本题主要考查了直线与平面平行的判定和直线与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案