题目内容
【题目】设函数![]() ,
,![]() ,且对所有的实数
,且对所有的实数![]() ,等式
,等式![]() 都成立,其
都成立,其![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() .
.
(1)如果函数![]() ,
,![]() ,求实数
,求实数![]() 的值;
的值;
(2)设函数![]() ,直接写出满足
,直接写出满足![]() 的两个函数
的两个函数![]() ;
;
(3)如果方程![]() 无实数解,求证:方程
无实数解,求证:方程![]() 无实解.
无实解.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,答案不唯一;(3)证明见解析.
,答案不唯一;(3)证明见解析.
【解析】
(1)根据已知条件![]() 直接代入计算即可;
直接代入计算即可;
(2)验证![]() 满足条件
满足条件![]() ,再者若
,再者若![]() ,则等式
,则等式![]() 也满足,由此可得出符合条件的函数
也满足,由此可得出符合条件的函数![]() 的两个不同的解析式;
的两个不同的解析式;
(3)假设方程![]() 有实数解,利用反证法推出与已知条件矛盾,进而证明结论成立.
有实数解,利用反证法推出与已知条件矛盾,进而证明结论成立.
(1)![]() ,
,![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,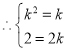 ,解得
,解得![]() ;
;
(2)若![]() ,则
,则![]() ,
,![]() ,此时
,此时![]() ;
;
若![]() ,则
,则![]() ,
,![]() ,此时
,此时![]() .
.
所以,当![]() 时,满足
时,满足![]() 的函数
的函数![]() 的两个解析式可以是
的两个解析式可以是![]() ,
,![]() (答案不唯一);
(答案不唯一);
(3)假设方程![]() 有实数解,设
有实数解,设![]() ,
,
则![]() ,
,![]() ,
,
两式相减得![]()
![]() ,所以,
,所以,![]() ,
,
由零点存在定理可知,存在![]() ,使得
,使得![]() ,
,
![]() 无实根,则
无实根,则![]() 永远不成立,推出假设不成立.
永远不成立,推出假设不成立.
所以,方程![]() 无实数解,方程
无实数解,方程![]() 也无实解.
也无实解.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() =bx+a;(其中
=bx+a;(其中 ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)