题目内容
已知a，b，c是直角三角形的三边，其中c为斜边，若实数M使不等式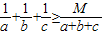
恒成立，则实数M的最大值是（ ）A．6+2
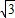
B．5
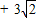
C．6
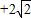
D．9
【答案】分析：由于a，b，c是直角三角形的三边，其中c为斜边，可设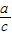
=sinα，则
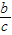=cosα，从而将
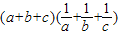转化为用三角函数指数进行解决．
解答：解：设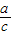
=sinα，则
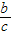=cosα
则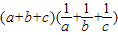
=
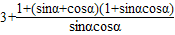
设t=sinα+cosα，则1＜t≤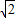
，sinαcosα=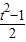
代入得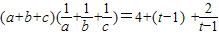
而f（x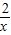）=x+
，在0＜x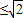
时单调递减，
所以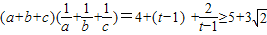
所以M最大值为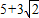
故选B
点评：本题以直角三角形为载体，考查基本不等式的运用，考查函数的单调性，同时考查了恒成立问题的处理．
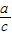=sinα，则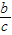=cosα，从而将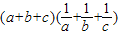转化为用三角函数指数进行解决．解答：解：设
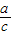=sinα，则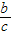=cosα则
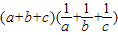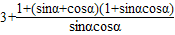
=设t=sinα+cosα，则1＜t≤
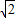，sinαcosα=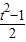代入得
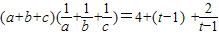
而f（x）=x+
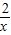，在0＜x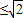时单调递减，所以
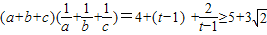
所以M最大值为
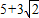
故选B
点评：本题以直角三角形为载体，考查基本不等式的运用，考查函数的单调性，同时考查了恒成立问题的处理．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目