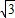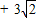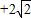题目内容
已知a,b,c是直角三角形的三边,其中c为斜边,若实数M使不等式
+
+
≥
恒成立,则实数M的最大值是( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| M |
| a+b+c |
A.6+2
| B.5+ 3
| C.6+2
| D.9 |
设
=sinα,则
=cosα
则(a+b+c)(
+
+
)=3+
设t=sinα+cosα,则1<t≤
,sinαcosα=
代入得(a+b+c)(
+
+
)=4+(t-1) +
而f(x)=x+
,在0<x≤
时单调递减,
所以(a+b+c)(
+
+
)=4+(t-1) +
≥5+3
所以M最大值为5+3
故选B
| a |
| c |
| b |
| c |
则(a+b+c)(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1+(sinα+cosα)(1+sinαcosα) |
| sinαcosα |
设t=sinα+cosα,则1<t≤
| 2 |
| t2-1 |
| 2 |
代入得(a+b+c)(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 2 |
| t-1 |
而f(x)=x+
| 2 |
| x |
| 2 |
所以(a+b+c)(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 2 |
| t-1 |
| 2 |
所以M最大值为5+3
| 2 |
故选B

练习册系列答案
相关题目
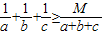 恒成立,则实数M的最大值是( )
恒成立,则实数M的最大值是( )