��Ŀ����
����Ŀ��ijӪ��ʦҪ��Ϊij����ͯԤ����ͺ����ͣ���֪һ����λ����ͺ�12����λ��̼ˮ�����6����λ�ĵ����ʺ�6����λ��ά����C��һ����λ�����ͺ�8����λ��̼ˮ�����6����λ�ĵ����ʺ�10����λ��ά����C�����⣬�ö�ͯ��������Ҫ��Ӫ״�����ٺ�64����λ��̼ˮ�������42����λ�ĵ����ʺ�54����λ��ά����C�����һ����λ����͡����͵ķ��÷ֱ���2.5Ԫ��4Ԫ����ôҪ����������Ӫ��Ҫ���һ������٣�Ӧ��Ϊ�ö�ͯ�ֱ�Ԥ�����ٸ���λ����ͺ����ͣ�
���𰸡��⣺��Ϊ�ö�ͯ�ֱ�Ԥ��x����λ����ͺ�y����λ�����ͣ�
�����ΪF����F=2.5x+4y��
������֪Լ������Ϊ�� 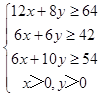
������������ͼ��
�任Ŀ�꺯���� ![]()
��Ŀ�꺯������A����ֱ��6x+6y=42��6x+10y=54�Ľ��㣨4��3��ʱ��Fȡ����Сֵ��
��Ҫ����Ӫ��Ҫ���һ������٣�Ӧ��Ϊ��ͯ�ֱ�Ԥ��4����λ����ͺ�3����λ�����ͣ�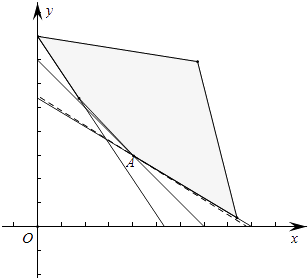
���������������Թ滮��˼�뷽�����ijЩʵ����������ֱ�߷��̵�һ��Ӧ�ã�������Ҫ�����ҳ�Լ��������Ŀ�꺯����ȷ���軭������������ͼ��ֱ�����������������Ž⣮

��ϰ��ϵ�д�
 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
�����Ŀ