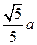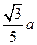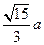题目内容
a为何值时,直线ax+(1-a)y+3=0与(a-1)x+(2a+3)y-2=0相交?平行?垂直?
两直线对任意a∈R恒相交,不可能平行. a=1或a=-3时两直线垂直.
由A1B2-A2B1=a(2a+3)-(a-1)(1-a)=3a2+a+1=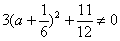 .
.
∴两直线对任意a∈R恒相交,不可能平行.
又∵当A1A2+B1B2=a(a-1)+(1-a)(2a+3)=0,即(a-1)(a+3)=0,也即a=1或a=-3时两直线垂直.
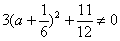 .
.∴两直线对任意a∈R恒相交,不可能平行.
又∵当A1A2+B1B2=a(a-1)+(1-a)(2a+3)=0,即(a-1)(a+3)=0,也即a=1或a=-3时两直线垂直.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,BC∥
,BC∥
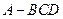 中,
中,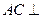 底面
底面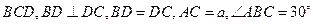 ,点
,点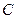 到平面
到平面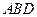 的距离是( ).
的距离是( ).