题目内容
17.己知函数f(x)=|x-a|,g(x)=ax,(a∈R).(1)若方程f(x)=g(x)有两个不同的解,求出实数a的取值范围;
(2)若a>0,记F(x)=g(x)f(x),试求函数y=F(x)在区间[1,2]的最大值.
分析 (1)分三种情况加以讨论:当a>0时,将方程f(x)=g(x)两边平方,得方程(x-a)2-a2x2=0在(0,+∞)上有两解,构造新函数h(x)=(a2-1)x2+2ax-a2,通过讨论h(x)图象的对称轴方程和顶点坐标,可得0<a<-1;当a<0时,用同样的方法得到-1<a<0;而当a=0时代入函数表达式,显然不合题意,舍去.最后综合实数a的取值范围;
(2)F(x)=f(x)•g(x)=ax|x-a|,根据实数a与区间[1,2]的位置关系,分4种情况加以讨论:
①当0<a≤1时,②当1<a≤2时,再讨论:当1<a<$\frac{5}{3}$时;当$\frac{5}{3}$≤a≤2时,y=F(x)的最大值为F(1)=a2-a;③当2<a≤4时,F(x)=-a(x2-ax),④当a>4时,F(x)=-a(x2-ax),运用单调性求得最大值,
最后综上所述,可得函数y=F(x)在区间[1,2]上的最大值的结论.
解答 解:(1)当a>0时,|x-a|-ax=0有两解,
等价于方程(x-a)2-a2x2=0在(0,+∞)上有两解,
即(a2-1)x2+2ax-a2=0在(0,+∞)上有两解,
令h(x)=(a2-1)x2+2ax-a2,
因为h(0)=-a2<0,所以$\left\{\begin{array}{l}{{a}^{2}-1<0}\\{\frac{a}{1-{a}^{2}}>0}\\{△=4{a}^{2}+4{a}^{2}({a}^{2}-1)>0}\end{array}\right.$,
故0<a<1;
同理,当a<0时,得到-1<a<0;
当a=0时,f(x)=|x|=0=g(x),显然不合题意,舍去.
综上可知实数a的取值范围是(-1,0)∪(0,1);
(3)令F(x)=f(x)•g(x),
①当0<a≤1时,则F(x)=a(x2-ax),
对称轴x=$\frac{a}{2}$,函数在[1,2]上是增函数,
所以此时函数y=F(x)的最大值为4a-2a2.
②当1<a≤2时,F(x)=$\left\{\begin{array}{l}{-a({x}^{2}-ax),1<x≤a}\\{a({x}^{2}-ax),a<x≤2}\end{array}\right.$,对称轴x=$\frac{a}{2}$,
所以函数y=F(x)在(1,a]上是减函数,在[a,2]上是增函数,
F(1)=a2-a,F(2)=4a-2a2,
1)若F(1)<F(2),即1<a<$\frac{5}{3}$,此时函数y=F(x)的最大值为4a-2a2;
2)若F(1)≥F(2),即$\frac{5}{3}$≤a≤2,此时函数y=F(x)的最大值为a2-a.
③当2<a≤4时,F(x)=-a(x2-ax)对称轴x=$\frac{a}{2}$,
此时Fmax(x)=F($\frac{a}{2}$)=$\frac{{a}^{3}}{4}$,
④当a>4时,对称轴x=$\frac{a}{2}$∈(2,+∞),此时F(x)max=F(2)=2a2-4a;
综上可知,函数y=F(x)在区间[1,2]上的最大值
F(x)=$\left\{\begin{array}{l}{4a-2{a}^{2},0<a<\frac{5}{3}}\\{{a}^{2}-a,\frac{5}{3}≤a≤2}\\{\frac{{a}^{3}}{4},2<a≤4}\\{2{a}^{2}-4a,a>4}\end{array}\right.$.
点评 本题借助于含有字母参数的一次函数和含有绝对值的函数,通过讨论它们的奇偶性和单调性,以及讨论含有参数的方程根的个数,着重考查了函数的单调性的奇偶性、函数的零点和二次函数的图象与性质等知识点,属于难题.请同学们注意分类讨论和数形结合的数学思想在解决本题中所起的作用.

 名校课堂系列答案
名校课堂系列答案(1)求数列{an},{bn}的通项公式.
(2)设cn=an•bn,求数列{cn}的前n项和Tn.
| A. | 8 | B. | 10 | C. | 9或10 | D. | 8和9 |
 三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)
三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小) 中,
中,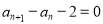 ,且
,且 ,则
,则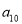 等于( )
等于( )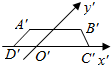 (1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.
(1)已知△ABC的三边长为a,b,c.判断△ABC的面积与△ABC的平面直观图△A′B′C′的面积的关系.