题目内容
2.过点M(3,2)的抛物线方程是( )| A. | x2=$\frac{9}{2}$y | B. | y2=$\frac{4}{3}$x | C. | y2=$\frac{4}{3}$x或 x2=$\frac{9}{2}$y | D. | y2=$\frac{3}{4}$x或x2=$\frac{2}{9}$y |
分析 设过点M(3,2)的抛物线方程是y2=2px,或x2=2p′y,把点M的坐标代入,求得p、p′的值,可得结论.
解答 解:设过点M(3,2)的抛物线方程是y2=2px,或x2=2p′y.
若抛物线方程是y2=2px,把M(3,2)代入可得4=2p×4,求得 p=$\frac{2}{3}$,
可得抛物线方程是y2=$\frac{4}{3}$x.
若抛物线的方程为x2=2p′y,把M(3,2)代入可得9=2p′×2,求得 p′=$\frac{9}{4}$,
可得抛物线方程是x2=$\frac{9}{2}$y.
故选:C.
点评 本题主要考查抛物线的标准方程,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
13.设i为虚数单位,复数$\frac{1+i}{2+bi}$为纯虚数,则实数b等于( )
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
11.已知偶函数f(x)对于任意x∈R都有f(x+1)=-f(x),且f(x)在区间[0,2]上是递增的,则f(-6.5),f(-1),f(0)的大小关系是( )
| A. | f(0)<f(-6.5)<f(-1) | B. | f(-6.5)<f(0)<f(-1) | C. | f(-1)<f(-6.5)<f(0) | D. | f(-1)<f(0)<f(-6.5) |
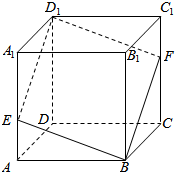 已知E,F分别是正方体A1B1C1D1-ABCD的棱AA1,CC1上的点,且A1E=2EA,CF=2FC1,求证:四边形BED1F是平行四边形.
已知E,F分别是正方体A1B1C1D1-ABCD的棱AA1,CC1上的点,且A1E=2EA,CF=2FC1,求证:四边形BED1F是平行四边形.