Question

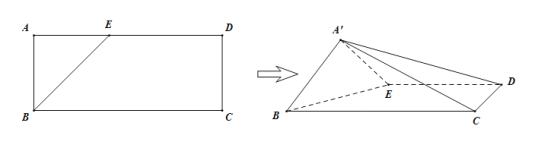
【题目】如图甲所示的平面五边形中，，，，，，现将图甲所示中的沿边折起，使平面平面得如图乙所示的四棱锥．在如图乙所示中

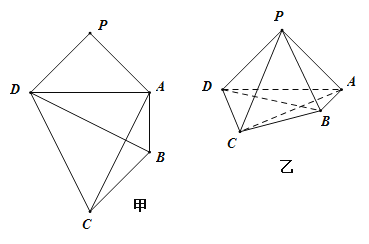
（1）求证：平面；

（2）求二面角的大小；

（3）在棱上是否存在点使得与平面所成的角的正弦值为？并说明理由．

Answer 1

【答案】（1）证明见解析；（2）；（3）存在，理由见解析.

【解析】

（1）推导出AB⊥AD，AB⊥平面PAD，AB⊥PD，PD⊥PA，由此能证明PD⊥平面PAB；

（2）取AD的中点O，连结OP， OC，由知OC⊥OA，以为坐标原点，OC所在的直线为x轴，OA所在的直线为y轴建立空间直角坐标系，利用向量法能求出二面角A-PB-C的大小；

（3）假设点M存在，其坐标为(x, y, z)，BM与平面PBC所成的角为，则存在λ∈(0， 1)，有，利用向量法能求出在棱PA上满足题意的点M存在．

（1）∵，，，

∴，

∴，

∵平面平面，平面平面，

∴平面，

又∵平面，

∴，

又∵，，

∴平面．

（2）取的中点，连结，，

由平面平面知平面，

由知，

以为坐标原点，所在的直线为轴，所在的直线为轴建立空间直角坐标系

如图所示，

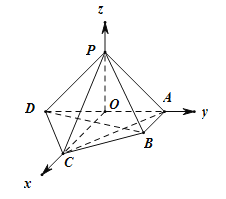
则易得，，，，，

设平面的法向量为，

由，得，

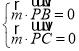令得，，

∴，

设二面角大小为，

则，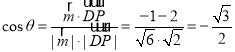

∵，

∴二面角的大小．

（3）假设点存在，其坐标为，与平面所成的角为，

则存在，有，

即，，

则，

从而化简得，

解得

∵，

∴

∴在棱上满足题意的点存在．