题目内容
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠DAB=∠ABC=
,且AB=BC=2AD=2,侧面PAB⊥底面ABCD,△PAB是等边三角形.
(1)求证:BD⊥PC;
(2)求二面角B-PC-D的大小.

| π |
| 2 |
(1)求证:BD⊥PC;
(2)求二面角B-PC-D的大小.

(1)取AB 中点为O,连接PO,CO,
∵△PAB 是等边三角形,
∴PO⊥AB,
又∵侧面PAB⊥底面ABCD,
∴PO⊥底面ABCD,
∴OC为PC在底面ABCD上的射影,
又∵AB=BC=2AD=2,∠ABC=∠DAB=
,
∴△DAB≌△OBC,∴∠BCO=∠DBA,
∴BD⊥OC,∴BD⊥PC.
(2)取PC中点E,连接BE,DE,
∵PB=BC,
∴BE⊥PC,
又∵BD⊥PC,BE∩BD=B,
∴PC⊥平面BDE
,∴PC⊥DE,
∴∠BED就是二面角B-PC-D的平面角.
∵AB=BC=2AD=2,∠ABC=
,
∴BE=PF=
PC=
,PD=BD=
,
∴DE=
,
∴BE2+DE2=BD2,
∴∠BED=
.
即二面角B-PC-D的大小为:
.
∵△PAB 是等边三角形,
∴PO⊥AB,
又∵侧面PAB⊥底面ABCD,

∴PO⊥底面ABCD,
∴OC为PC在底面ABCD上的射影,
又∵AB=BC=2AD=2,∠ABC=∠DAB=
| π |
| 2 |
∴△DAB≌△OBC,∴∠BCO=∠DBA,
∴BD⊥OC,∴BD⊥PC.
(2)取PC中点E,连接BE,DE,
∵PB=BC,
∴BE⊥PC,
又∵BD⊥PC,BE∩BD=B,
∴PC⊥平面BDE
,∴PC⊥DE,
∴∠BED就是二面角B-PC-D的平面角.
∵AB=BC=2AD=2,∠ABC=
| π |
| 2 |
∴BE=PF=
| 1 |
| 2 |
| 2 |
| 5 |
∴DE=
| 3 |
∴BE2+DE2=BD2,
∴∠BED=
| π |
| 2 |
即二面角B-PC-D的大小为:
| π |
| 2 |

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目





 的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A、B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若
的右焦点为F,过点F作与x轴垂直的直线l交两渐近线于A、B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若 ,
, ,则该双曲线的离心率为( )
,则该双曲线的离心率为( ) B.2 C.
B.2 C.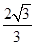 D.
D.
 的方程有
的方程有 ,则
,则


 =
=
 ,用
,用 ,
, 表示
表示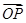 ,则
,则
