题目内容
已知函数f(x)是定义在R上的偶函数,且x≥0时, .
.(I)求f(-1)的值;
(II)求函数f(x)的值域A;
(III)设函数
 的定义域为集合B,若A⊆B,求实数a的取值范围.
的定义域为集合B,若A⊆B,求实数a的取值范围.
【答案】分析:(I)根据函数是偶函数,把-1转化到给出解析式的范围上,代入解析式可求.
(II)因为f(x)是定义在R上的偶函数,所以x≥0时函数值的取值集合就是函数f(x)的值域A,求出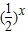 (x≥0)的取值集合即可.
(x≥0)的取值集合即可.
(III)先写出x所要满足的一元二次不等式,因为A=(0,1]⊆B,
法一:把不等式分解因式,很容易看出两根,一根为-1又B中含有正数,所以另一根一定大于-1得定义域B=[-1,a],得实数a的取值范围;
法二:设为函数,利用函数图象,(0,1]在图象与x轴的两交点之间,图象开中向上,x=0,x=1时对应的函数小于等于0,得不等式组,可求实数a的取值范围.
解答:解:(I)∵函数f(x)是定义在R上的偶函数
∴f(-1)=f(1)
又x≥0时,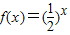
∴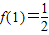 ,即f(-1)=
,即f(-1)= .
.
(II)由函数f(x)是定义在R上的偶函数,
可得函数f(x)的值域A即为
x≥0时,f(x)的取值范围,
当x≥0时,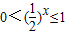
故函数f(x)的值域A=(0,1].
(III)∵
定义域B={x|-x2+(a-1)x+a≥0}={x|x2-(a-1)x-a≤0}
方法一:由x2-(a-1)x-a≤0得(x-a)(x+1)≤0
∵A⊆B∴B=[-1,a],且a≥1(13分)
∴实数a的取值范围是{a|a≥1}
方法二:设h(x)=x2-(a-1)x-a
A⊆B当且仅当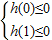 即
即
∴实数a的取值范围是{a|a≥1}
点评:本题考查函数的奇偶性,集合包含关系的判断,函数值域,函数的奇偶性在求相反两个自变量的函数值时很好用,在求值域上也可只求y轴一侧的,由集合的包含关系求参数范围时,用端点比较法,结合图象,更好理解.
(II)因为f(x)是定义在R上的偶函数,所以x≥0时函数值的取值集合就是函数f(x)的值域A,求出
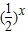 (x≥0)的取值集合即可.
(x≥0)的取值集合即可.(III)先写出x所要满足的一元二次不等式,因为A=(0,1]⊆B,
法一:把不等式分解因式,很容易看出两根,一根为-1又B中含有正数,所以另一根一定大于-1得定义域B=[-1,a],得实数a的取值范围;
法二:设为函数,利用函数图象,(0,1]在图象与x轴的两交点之间,图象开中向上,x=0,x=1时对应的函数小于等于0,得不等式组,可求实数a的取值范围.
解答:解:(I)∵函数f(x)是定义在R上的偶函数
∴f(-1)=f(1)
又x≥0时,
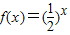
∴
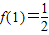 ,即f(-1)=
,即f(-1)= .
.(II)由函数f(x)是定义在R上的偶函数,
可得函数f(x)的值域A即为
x≥0时,f(x)的取值范围,
当x≥0时,
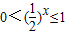
故函数f(x)的值域A=(0,1].
(III)∵

定义域B={x|-x2+(a-1)x+a≥0}={x|x2-(a-1)x-a≤0}
方法一:由x2-(a-1)x-a≤0得(x-a)(x+1)≤0
∵A⊆B∴B=[-1,a],且a≥1(13分)
∴实数a的取值范围是{a|a≥1}
方法二:设h(x)=x2-(a-1)x-a
A⊆B当且仅当
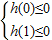 即
即
∴实数a的取值范围是{a|a≥1}
点评:本题考查函数的奇偶性,集合包含关系的判断,函数值域,函数的奇偶性在求相反两个自变量的函数值时很好用,在求值域上也可只求y轴一侧的,由集合的包含关系求参数范围时,用端点比较法,结合图象,更好理解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知函数f(x)=x+
已知函数f(x)=x+