题目内容
设复数z1=1+2ai,z2=a-i(a∈R),A={z||z-z1|<
},B={z||z-z2|≤2
},已知A∩B=∅,则a的取值范围是
| 2 |
| 2 |
a≤-2或a≥
| 8 |
| 5 |
a≤-2或a≥
.| 8 |
| 5 |
分析:利用复数的减法的几何意义可得:集合A是以O1(1,2a)为圆心,r=
为半径的圆的内部的点所对应的复数集合;集合B是以O2(a,-1)为圆心,R=2
为半径的圆周及其内部的点所对应的复数集合.由已知A∩B=∅,可得|O1O2|≥R+r.解出即可.
| 2 |
| 2 |
解答:解:∵复数z1=1+2ai,z2=a-i(a∈R),
∴|z-z1|<
即|z-(1+2ai)|<
;
|z-z2|≤2
,即|z-(a-i)|≤2
.
由复数的减法的几何意义可得:集合A是以O1(1,2a)为圆心,r=
为半径的圆的内部的点所对应的复数集合;
集合B是以O2(a,-1)为圆心,R=2
为半径的圆周及其内部的点所对应的复数集合.
∵A∩B=∅,∴|O1O2|≥R+r.
∴
≥3
.
解得a≤-2或a≥
.
故答案为a≤-2或a≥
.
∴|z-z1|<
| 2 |
| 2 |
|z-z2|≤2
| 2 |
| 2 |
由复数的减法的几何意义可得:集合A是以O1(1,2a)为圆心,r=
| 2 |
集合B是以O2(a,-1)为圆心,R=2
| 2 |
∵A∩B=∅,∴|O1O2|≥R+r.
∴
| (1-a)2+(2a+1)2 |
| 2 |
解得a≤-2或a≥
| 8 |
| 5 |
故答案为a≤-2或a≥
| 8 |
| 5 |
点评:熟练掌握复数的减法的几何意义、圆的标准方程、交集的运算、一元二次不等式的解法等是解题的关键.

练习册系列答案
相关题目
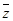 及|
及|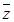 及|
及|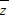 及|
及|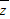 |;
|;