题目内容

12．求下列函数的值域：
（1）y=2x+1，x∈{1，2，3，4，5}；
（2）y=$\sqrt{x}$+1．

分析 （1）分别让x取1，2，3，4，5，然后求出对应的y值，从而得出该函数的值域；
（2）由$\sqrt{x}≥0$，从而可得到y≥1，这便求出了该函数的值域．

解答 解：（1）x=1，2，3，4，5时，对应的y=3，5，7，9，11；
∴该函数的值域为：{3，5，7，9，11}；
（2）$\sqrt{x}≥0$，∴$\sqrt{x}+1≥1$；
∴该函数的值域为[1，+∞）．

点评 考查函数值域的概念，定义域为孤立实数的值域的求法，以及根据不等式的性质求值域．

练习册系列答案
相关题目
2．写出表示下列平面区域的二元一次不等式组：
（1）△ABC的三条边围成的平面区域（包括三角形的三条边），其中点A（-2，1），B（5，1），C（3，4）．
（2）点A（-1，1），B（2，-1）是正方形ABCD（字母A，B，C，D依逆时针顺序排列）的两个顶点，正方形ABCD的四条边围成的平面区域（不包括正方形的四条边）．
3．已知x≠0．函数f（x）满足f（x-$\frac{1}{x}$）=x2+$\frac{1}{{x}^{2}}$，则f（x）=x2+2．
20．已知函数f：A→B（A，B为非空数集），定义域为M，值域为N，则A，B，M，N的关系是（　　）
A．M=A，N=BB．M⊆A，N=BC．M=A，N⊆BD．M⊆A，N⊆B
7．已知函数f（x）=x2-2x+3．则f（t2+2）与3的大小关系为f（t2+2）≥3．
17．已知M={m|m=2k，k∈Z}，X={x|x=2k+1，k∈Z}．Y={y|y=4k+1，k∈Z}，则（　　）
A．x+y∈MB．x+y∈XC．x+y∈YD．x+y∉M
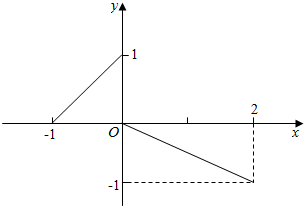
4．某市去年11月份曾发生流感，据资料记载，11月1日，该市新的流感病毒感染者有20人，以后，每天的新感染者平均比前一天的新感染者增加50人，问11月10日，该市感染此病毒的新患者人数是多少？并求这十天患者的总人数．
1．f（x）图象如图，则f（x）=$\left\{\begin{array}{l}{x+1}&{-1≤x≤0}\\{-\frac{1}{2}x}&{0＜x≤2}\end{array}\right.$．
1．已知单位向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为120°，且|$\overrightarrow{c}$-$\overrightarrow{a}$|+|$\overrightarrow{c}$-$\overrightarrow{b}$|=$\sqrt{3}$，则|$\overrightarrow{c}$+2$\overrightarrow{a}$|的取值范围是（　　）
A．[$\frac{3}{2}$，+∞）B．[$\sqrt{3}$，3]C．[$\sqrt{3}$，+∞）D．[$\frac{3}{2}$，3]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网