题目内容
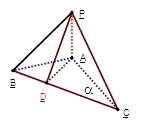 如图BC是Rt△ABC的斜边,过A作△ABC所在平面a垂线AP,连PB、PC,过A作AD⊥BC于D,连PD,那么图中直角三角形的个数是
如图BC是Rt△ABC的斜边,过A作△ABC所在平面a垂线AP,连PB、PC,过A作AD⊥BC于D,连PD,那么图中直角三角形的个数是
- A.4个
- B.6个
- C.7个
- D.8个
D
分析:利用AP⊥面ABC,Rt△ABC,AD是PD在面ABC内的射影,故由AD⊥BC可得PD⊥BC.
解答:∵BC是Rt△ABC的斜边,
A作△ABC所在平面a垂线AP,AD⊥BC于D,
图中直角三角形有:
△ABC,△PAB,△PAD,△PAC,△ADB,△ADC,△PDB,△PDC 共8个,
故选D.
点评:本题考查三垂线定理的应用,以及棱锥的结构特征,体现数形结合的数学思想.
分析:利用AP⊥面ABC,Rt△ABC,AD是PD在面ABC内的射影,故由AD⊥BC可得PD⊥BC.
解答:∵BC是Rt△ABC的斜边,
A作△ABC所在平面a垂线AP,AD⊥BC于D,
图中直角三角形有:
△ABC,△PAB,△PAD,△PAC,△ADB,△ADC,△PDB,△PDC 共8个,
故选D.
点评:本题考查三垂线定理的应用,以及棱锥的结构特征,体现数形结合的数学思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
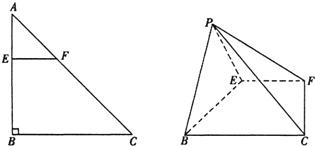
 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.