题目内容
如图，以Rt△ABC的直角边AB为直径的半圆O，与斜边AC交于D，E是BC边上的中点，连接DE．（1）DE与半圆O相切吗？若相切，请给出证明；若不相切，请说明理由；
（2）若AD、AB的长是方程x2-10x+24=0的两个根，求直角边BC的长．
分析：（1）连OD，OE，由E是BC边上的中点，得到OE是△ABC的中位线，则OE∥AC，所以有∠1=∠3，∠2=∠A，而∠A=∠3，因此得到∠1=∠2，再加上OD=OB，OE为公共边，所以得到△OED≌△OEB，于是∠OED=∠OBE=90°．
（2）首先证明△ABC∽△ADB，得出
=
，根据AD、AB的长是方程x2-10x+24=0的两个根，可得AD=4、AB=6，
从而可求AC的长，由此可求BC的长．
（2）首先证明△ABC∽△ADB，得出
| AB |
| AC |
| AD |
| AB |
从而可求AC的长，由此可求BC的长．
解答：（1）解：DE与半圆O相切
证明：连OD，OE，如图，
∵E是BC边上的中点，AB是半圆O的直径，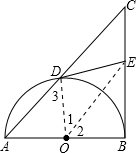
∴OE是△ABC的中位线，
∴OE∥AC，
∴∠1=∠3，∠2=∠A，而OD=OA，∠A=∠3
∴∠1=∠2，
又∵OD=OB，OE为公共边，
∴△OED≌△OEB，
∴∠ODE=∠OBE=90°．
∴DE与半圆O相切．
（2）解：∵AB为直径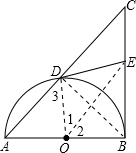
∴∠ADB=∠ABC=90°，∠CAB=∠CAB，
∴△ABC∽△ADB．
∴
=
，
∵AD、AB的长是方程x2-10x+24=0的两个根
∴解方程x2-10x+24=0得x1=4，x2=6
∵AD＜AB
∴AD=4、AB=6，
∴AC=9，
在直角三角形ABC中，AB=6，AC=9
∴BC=
=3
．
证明：连OD，OE，如图，
∵E是BC边上的中点，AB是半圆O的直径，
∴OE是△ABC的中位线，
∴OE∥AC，
∴∠1=∠3，∠2=∠A，而OD=OA，∠A=∠3
∴∠1=∠2，
又∵OD=OB，OE为公共边，
∴△OED≌△OEB，
∴∠ODE=∠OBE=90°．
∴DE与半圆O相切．
（2）解：∵AB为直径
∴∠ADB=∠ABC=90°，∠CAB=∠CAB，
∴△ABC∽△ADB．
∴
| AB |
| AC |
| AD |
| AB |
∵AD、AB的长是方程x2-10x+24=0的两个根
∴解方程x2-10x+24=0得x1=4，x2=6
∵AD＜AB
∴AD=4、AB=6，
∴AC=9，
在直角三角形ABC中，AB=6，AC=9
∴BC=
| AC2-AB2 |
| 5 |
点评：本题考查的重点是圆的切线的判定方法以及相似三角形的性质与判定，解题的关键是利用经过半径的外端点与半径垂直的直线是圆的切线．
练习册系列答案
相关题目
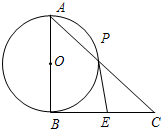选修4-1：几何证明选讲
