题目内容
如图,D是Rt△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.
(1)证明sinα+cos2β=0;
(2)若AC=
DC,求β的值.
(1)证明:如题图，因为α=
-∠BAD=-(π-2β)=2β-
,
所以sinα=sin(2β-
)=-cos2β,
即sinα+cos2β=0.
(2)解:在△ADC中,由正弦定理得
,即
.所以sinβ=
sinα.
由(1),sinα=-cos2β,所以sinβ=-
cos2β=-
(1-2sin2β),
即2
sin2β-sinβ-
=0.
解得sinβ=
或sinβ=-
.
因为0＜β＜
,所以sinβ=
.从而β=
.
练习册系列答案
相关题目
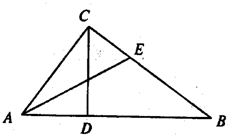如图，在Rt△ABC中，∠C是直角，AC=3，BC=4，CD⊥AB于点D，∠A的平分线交CD于点M，交BC于点E，求：
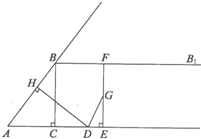如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BBl∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．
（2012•许昌三模）如图，在RT△ABC中，D是斜边AB上一点，且AC=AD，记∠BCD=β，∠ABC=α．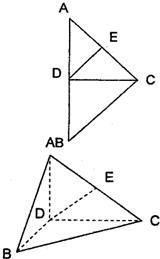
如图，在Rt△ABC中，∠ACB=90°，AC=BC=4，D是AB中点，E是AC的中点，现将△ABC沿CD翻折成直二面角A-DC-B．