题目内容
在直角坐标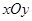 中,圆
中,圆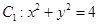 ,圆
,圆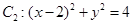 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆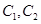 的极坐标方程,并求出圆
的极坐标方程,并求出圆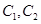 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求出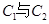 的公共弦的参数方程。
的公共弦的参数方程。
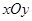 中,圆
中,圆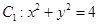 ,圆
,圆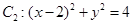 。
。(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆
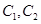 的极坐标方程,并求出圆
的极坐标方程,并求出圆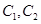 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);(Ⅱ)求出
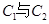 的公共弦的参数方程。
的公共弦的参数方程。见解析
(Ⅰ)圆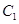 的极坐标方程为
的极坐标方程为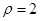 圆
圆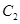 的极坐标方程为
的极坐标方程为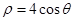
解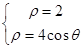 得
得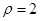 ,
,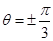
故圆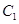 与圆
与圆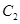 交点的坐标为
交点的坐标为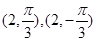
注:极坐标系下点的表示不唯一
(Ⅱ)(解法一)
由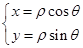 得圆
得圆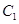 与圆
与圆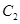 交点的直角坐标分别为
交点的直角坐标分别为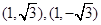
故圆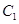 与圆
与圆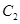 的公共弦的参数方程为
的公共弦的参数方程为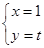
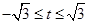
(或参数方程写成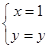
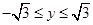 )
)
(解法二)
将x=1代入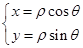 得
得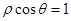 ,从而
,从而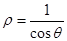
于是圆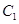 与圆
与圆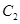 的公共弦的参数方程为
的公共弦的参数方程为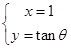
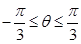
考点定位:本大题主要考查直角坐标系与极坐标系之间的互化,意在考查考生利用坐标之间的转化求解。
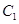 的极坐标方程为
的极坐标方程为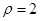 圆
圆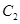 的极坐标方程为
的极坐标方程为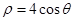
解
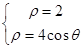 得
得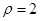 ,
,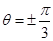
故圆
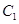 与圆
与圆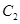 交点的坐标为
交点的坐标为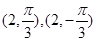
注:极坐标系下点的表示不唯一
(Ⅱ)(解法一)
由
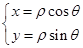 得圆
得圆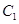 与圆
与圆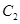 交点的直角坐标分别为
交点的直角坐标分别为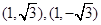
故圆
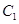 与圆
与圆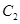 的公共弦的参数方程为
的公共弦的参数方程为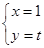
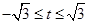
(或参数方程写成
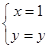
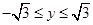 )
)(解法二)
将x=1代入
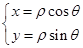 得
得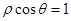 ,从而
,从而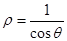
于是圆
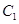 与圆
与圆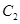 的公共弦的参数方程为
的公共弦的参数方程为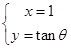
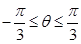
考点定位:本大题主要考查直角坐标系与极坐标系之间的互化,意在考查考生利用坐标之间的转化求解。

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
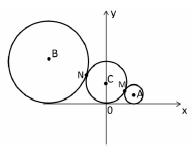
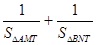 的最小值为2,求直线AB的方程.
的最小值为2,求直线AB的方程.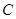 :
: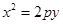 (
(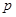 >0)的焦点为
>0)的焦点为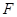 ,准线为
,准线为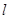 ,
,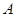 为
为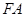 为半径的圆
为半径的圆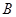 ,
,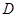 两点.
两点.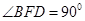 ,
,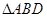 的面积为
的面积为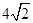 ,求
,求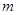 上,直线
上,直线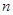 与
与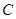 过点
过点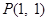 ,且与圆
,且与圆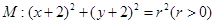 关于直线
关于直线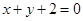 对称.
对称.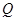 为圆
为圆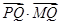 的最小值;
的最小值;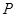 作两条相异直线分别与圆
作两条相异直线分别与圆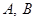 ,且直线
,且直线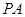 和
和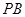 直线的倾斜角互补,
直线的倾斜角互补,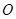 为坐标原点,试判断直线
为坐标原点,试判断直线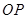 和
和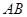 是否平行,并说明理由.
是否平行,并说明理由.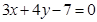 截曲线
截曲线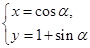 (
(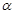 为参数)的弦长为_ _
为参数)的弦长为_ _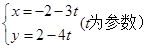 它与曲线C:
它与曲线C: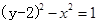 交于A、B两点。
交于A、B两点。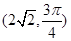 ,求点P到线段AB中点M的距离。
,求点P到线段AB中点M的距离。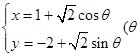 是参数)相切,则b= 。
是参数)相切,则b= 。 作圆
作圆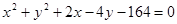 的弦,其中弦长为整数的共有( )
的弦,其中弦长为整数的共有( )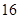 条
条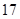 条
条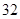 条
条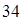 条
条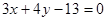 与圆
与圆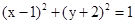 的位置关系是( )
的位置关系是( )