题目内容
【题目】已知a为实数，函数
.请讨论函数
单调性.
【答案】见解析
【解析】
由条件，知函数
的定义域为
.
若
，则
.
故
令
，得
（负值舍去）.
记
于是，在区间（0，b）上单调递减，在区间
上单调递增.
若a>0，则
先讨论
的单调性.
注意到
.
令
，得
.
当b>a，即a<1时，g（x）在区间（a，b）上单调递减，在区间上单调递增；
当
，即
时，
在区间
上单调递增.
再讨论
的单调性.
注意到，
.
当
，即
时，
，
在区间
上单调递减.
当
，即
时，令
，得
，
.
则在区间（0，c），（d，a）上分别单调递减，在区间（c，d）上单调递增.
综上，当a<1时，在区间（0，b）上单调递减，在区间上单调递增；
当
时，在区间（0，a）上单调递减，在区间上单调递增；
当时，在区间（0，c），（d，a）上分别单调递减，在区间（c，d），上单调递增.
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
【题目】一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位辆)，若按A,B,C三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A类轿车有10辆
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
（1）求下表中z的值；
（2）用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下：94,86,92,96,87,93,90,82把这8辆轿车的得分看作一个总体,从中任取一个得分数
记这8辆轿车的得分的平均数为
，定义事件
{
，且函数
没有零点}，求事件
发生的概率
【题目】某同学用“五点法”画函数
在某一个周期内的图像时，列表并填入了部分数据，如下表：
|
|
| |||
| 0 |
|
|
|
|
| 0 | 3 | 0 | 0 |
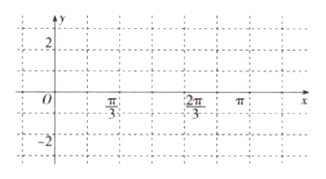
（1）请将上表数据补充完整，并写出函数
的解析式（直接写出结果即可）；
（2）根据表格中的数据作出在一个周期内的图像；
（3）求函数在区间
上的最大值和最小值.
【题目】统计学中，经常用环比、同比来进行数据比较，环比是指本期统计数据与上期比较，如
年
月与年
月相比，同比是指本期数据与历史同时期比较，如年月与
年月相比.
环比增长率
（本期数
上期数）
上期数
，
同比增长率（本期数同期数）同期数.
下表是某地区近
个月来的消费者信心指数的统计数据：
序号 |
|
|
|
|
|
|
|
|
时间 |
|
|
|
|
|
|
|
|
消费者信心指数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017年
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
求该地区
年
月消费者信心指数的同比增长率（百分比形式下保留整数）；
除年
月以外，该地区消费者信心指数月环比增长率为负数的有几个月？
由以上数据可判断，序号
与该地区消费者信心指数
具有线性相关关系，写出关于的线性回归方程
（
，
保留
位小数），并依此预测该地区年月的消费者信心指数（结果保留位小数，参考数据与公式：
，
，
，
，
）
