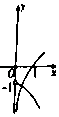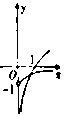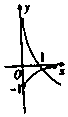题目内容
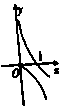
【题目】已知函数f(x)=x|2a﹣x|+2x,a∈R.
(1)若a=0,判断函数y=f(x)的奇偶性,并加以证明;
(2)若函数f(x)在R上是增函数,求实数a的取值范围;
(3)若存在实数a∈[﹣2,2],使得关于x的方程f(x)﹣tf(2a)=0有三个不相等的实数根,求实数t的取值范围.
【答案】
(1)解:函数y=f(x)为奇函数.
理由:当a=0时,f(x)=x|x|+2x,
f(﹣x)=﹣x|x|﹣2x=﹣f(x),
∴函数y=f(x)为奇函数
(2)解:f(x)= 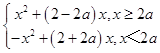 ,
,
当x≥2a时,f(x)的对称轴为:x=a﹣1;
当x<2a时,y=f(x)的对称轴为:x=a+1;
∴当a﹣1≤2a≤a+1时,f(x)在R上是增函数,
即﹣1≤a≤1时,函数f(x)在R上是增函数
(3)解:方程f(x)﹣tf(2a)=0的解即为方程f(x)=tf(2a)的解.
①当﹣1≤a≤1时,函数f(x)在R上是增函数,
∴关于x的方程f(x)=tf(2a)不可能有三个不相等的实数根;
②当a>1时,即2a>a+1>a﹣1,
∴f(x)在(﹣∞,a+1)上单调增,
在(a+1,2a)上单调减,在(2a,+∞)上单调增,
∴当f(2a)<tf(2a)<f(a+1)时,
关于x的方程f(x)=tf(2a)有三个不相等的实数根;
即4a<t4a<(a+1)2,
∵a>1,
∴1<t< ![]() (a+
(a+ ![]() +2).
+2).
设h(a)= ![]() (a+
(a+ ![]() +2),
+2),
∵存在a∈[﹣2,2],
使得关于x的方程f(x)=tf(2a)有三个不相等的实数根,
∴1<t<h(a)max,
又可证h(a)= ![]() (a+
(a+ ![]() +2)在(1,2]上单调增,
+2)在(1,2]上单调增,
∴<h(a)max= ![]() ,
,
∴1<t< ![]() ,
,
③当a<﹣1时,即2a<a﹣1<a+1,
∴f(x)在(﹣∞,2a)上单调增,
在(2a,a﹣1)上单调减,在(a﹣1,+∞)上单调增,
∴当f(a﹣1)<tf(2a)<f(2a)时,
关于x的方程f(x)=tf(2a)有三个不相等的实数根;
即﹣(a﹣1)2<t4a<4a,
∵a<﹣1,
∴1<t<﹣ ![]() (a+
(a+ ![]() ﹣2),
﹣2),
设g(a)=﹣ ![]() (a+
(a+ ![]() ﹣2),
﹣2),
∵存在a∈[﹣2,2],使得关于x的方程f(x)=tf(2a)有三个不相等的实数根,
∴1<t<g(a)max,
又可证g(a)=﹣ ![]() (a+
(a+ ![]() ﹣2)在[﹣2,﹣1)上单调减,
﹣2)在[﹣2,﹣1)上单调减,
∴g(a)max= ![]() ,
,
∴1<t< ![]() ;
;
综上:1<t< ![]() .
.
【解析】(1)若a=0,根据函数奇偶性的定义即可判断函数y=f(x)的奇偶性;(2)根据函数单调性的定义和性质,利用二次函数的性质即可求实数a的取值范围;(3)根据方程有三个不同的实数根,建立条件关系即可得到结论.
【考点精析】解答此题的关键在于理解奇偶性与单调性的综合的相关知识,掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性.

【题目】某百货公司1~6月份的销售量x与利润y的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(参考公式: ![]() =
= 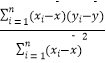 )=
)= 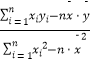 ,
, ![]() .
.
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程 ![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?