题目内容
设n为自然数,f(n)=1+(1)试证:若m、n∈N*且m<n,则f(n)≥f(m)+![]() ,并指出取等号的条件;
,并指出取等号的条件;
(2)计算得f(2)=![]() ,f(4)>2,f(8)>
,f(4)>2,f(8)>![]() ,f(16)>3,f(32)>
,f(16)>3,f(32)>![]() ,观察上述结果,推测一般的不等式,并用数学归纳法证明.
,观察上述结果,推测一般的不等式,并用数学归纳法证明.
(1)证明:由m<n,得
f(n)-f(m)=(1+![]() +…+
+…+![]() )-(1+
)-(1+![]() +…+
+…+![]() )=
)=![]() +
+![]() +…+
+…+![]() ≥
≥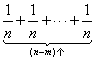 =
=![]() .
.
∴f(n)≥f(m)+![]() ,其中当且仅当n-m=1时,等号成立.
,其中当且仅当n-m=1时,等号成立.
(2)解:由f(2)≥![]() ,f(22)>2=
,f(22)>2=![]() ,f(8)=f(23)>
,f(8)=f(23)>![]() ,f(16)=f(24)>3=
,f(16)=f(24)>3=![]() ,f(32)=f(25)>
,f(32)=f(25)>![]() ,推测当n∈N*时,f(2n)≥
,推测当n∈N*时,f(2n)≥![]() ,下面用数学归纳法证明:
,下面用数学归纳法证明:
①当n=2时,f(22)=![]() >
>![]() ,不等式成立.
,不等式成立.
②假设n=k(k≥2)时,不等式成立,即f(2k)≥![]() .
.
那么f(2k+1)≥f(2k)+![]() ≥
≥![]() +
+![]() =
=![]() =
=![]() ,
,
即当n=k+1时,f(2k+1)≥![]() ,命题成立.
,命题成立.
根据①②可得对于n≥2的自然数n命题成立.

练习册系列答案
相关题目
