题目内容
已知函数y=2sinx(sinx+cosx)-1(1)求函数的最小正周期
(2)求函数的递增区间
(3)画出此函数在区间[-
| π |
| 2 |
| π |
| 2 |
分析:(1)首先整理函数的式子,进行三角函数式的恒等变换,先相乘,再用二倍角公式进行降幂,再利用辅角公式写出最简结果,用周期公式做出周期.
(2)根据正弦曲线的递增区间,写出使得函数的角在这一个区间上,解出其中的x的值,求出函数的单调区间.
(3)根据所给的区间,列出表格,取出几个关键点,画出坐标系,在坐标系中描出各个点,用光滑曲线把点连接起来,单调函数的图象.
(2)根据正弦曲线的递增区间,写出使得函数的角在这一个区间上,解出其中的x的值,求出函数的单调区间.
(3)根据所给的区间,列出表格,取出几个关键点,画出坐标系,在坐标系中描出各个点,用光滑曲线把点连接起来,单调函数的图象.
解答:解:(1)y=2sinx(sinx+cosx)-1=2sin2x+2sinxcosx-1
=sin2x-cos2x
=
sin(2x-
)
∴最小正周期为π
(2)根据正弦曲线的递增区间知当2x-
∈[2kπ-
,2kπ+
]
即x∈[kπ-
,kπ+
]
∴函数的递增区间是[kπ-
,kπ+
],(k∈z)
(3)首先列出表格
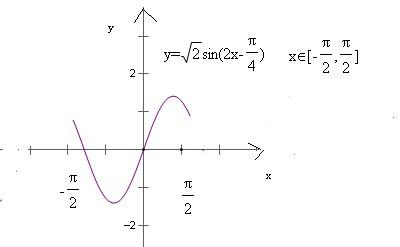
=sin2x-cos2x
=
| 2 |
| π |
| 4 |
∴最小正周期为π
(2)根据正弦曲线的递增区间知当2x-
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
即x∈[kπ-
| π |
| 8 |
| 3π |
| 8 |
∴函数的递增区间是[kπ-
| π |
| 8 |
| 3π |
| 8 |
(3)首先列出表格
| x | -
|
-
|
|
|
| ||||||||||
2x-
|
-
|
-
|
0 |
|
| ||||||||||
| y | 1 | -
|
0 |
|
1 |

点评:本题考查三角函数的变换和三角函数的性质,这是一个非常适合作为高考题目的题,这种题目注意三角恒等变换时不要出错,不然后面的运算都会出错.

练习册系列答案
相关题目
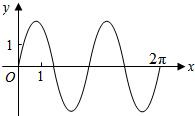 已知函数y=2sin(ωx+φ)(ω>0))在区间[0,2π]的图象如图:那么ω=( )
已知函数y=2sin(ωx+φ)(ω>0))在区间[0,2π]的图象如图:那么ω=( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知函数y=2sin(wx+θ)为偶函数,其图象与直线y=2某两个交点的横坐标分别为x1,x2,若|x2-x1|的最小值为π,则该函数在区间( )上是增函数.
A、(-
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
 下列4个命题:
下列4个命题: