题目内容
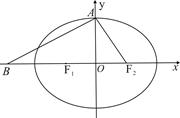
已知双曲线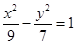 与椭圆
与椭圆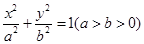 有相同的焦点,点
有相同的焦点,点 、
、 分别是椭圆的右、右顶点,若椭圆经过点
分别是椭圆的右、右顶点,若椭圆经过点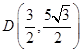 .
.
(1)求椭圆的方程;
(2)已知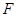 是椭圆的右焦点,以
是椭圆的右焦点,以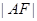 为直径的圆记为
为直径的圆记为 ,过点
,过点 引圆
引圆 的切线,求此切线的方程;
的切线,求此切线的方程;
(3)设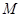 为直线
为直线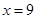 上的点,
上的点,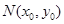 是圆
是圆 上的任意一点,是否存在定点
上的任意一点,是否存在定点 ,使得
,使得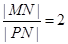 ?若存在,求出定点
?若存在,求出定点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(Ⅰ)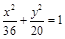 .(Ⅱ)
.(Ⅱ) .(Ⅲ)存在定点
.(Ⅲ)存在定点
解析试题分析:(Ⅰ)依题意,
 ,
,
所以椭圆的方程为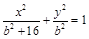 ,
,
代入D点坐标,解得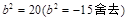 ,由此得
,由此得 ,
,
所以椭圆的方程为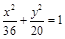 . (4分)
. (4分)
(Ⅱ)由(Ⅰ)知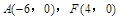 ,故圆
,故圆 的方程为
的方程为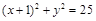 ,
,
则由 知,点
知,点 在圆
在圆 上,
上,
因为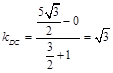 ,所以切线的斜率为
,所以切线的斜率为 ,
,
故所求切线的方程为 ,
,
即 . (8分)
. (8分)
(Ⅲ)设 ,假设存在点
,假设存在点 满足题意,
满足题意,
则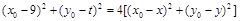 ,
,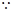 点
点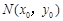 在圆C:
在圆C: 上,
上,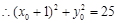 ,
,
化简得 ,
,
因为该式对任意的 恒成立,则
恒成立,则 解得
解得
故存在定点 对于直线
对于直线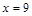 上的点
上的点 及圆
及圆 上的任意一点
上的任意一点 使得
使得 成立. (12分)
成立. (12分)
考点:本题考查了椭圆方程及直线与圆的位置关系
点评:从近几年课标地区的高考命题来看,解析几何综合题主要考查直线和圆锥曲线的位置关系以及范围、最值、定点、定值、存在性等问题,直线与多种曲线的位置关系的综合问题将会逐步成为今后命题的热点,尤其是把直线和圆的位置关系同本部分知识的结合,将逐步成为今后命题的一种趋势.近几年高考题中经常出现了以函数、平面向量、导数、数列、不等式、平面几何、数学思想方法等知识为背景,综合考查运用圆锥曲线的有关知识分析问题、解决问题的能力,试题风格每年都有所创新,但总体稳定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
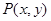 到定点
到定点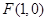 的距离比它到
的距离比它到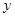 轴的距离大
轴的距离大 。
。 的轨迹
的轨迹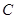 的方程;
的方程;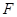 的直线
的直线 与
与 两点,若
两点,若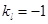 ,求弦
,求弦 的长。
的长。 到点
到点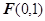 的距离与点
的距离与点 轴的距离的差等于1.(I)求动点
轴的距离的差等于1.(I)求动点 的方程;(II)过点
的方程;(II)过点 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ,设
,设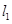 与轨迹
与轨迹 ,
, 与轨迹
与轨迹 ,求
,求 的最小值.
的最小值. :
: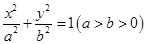 的一个焦点为
的一个焦点为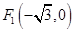 且过点
且过点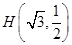 .
.
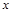 轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.
轴于点N,M,若直线OT与过点M,N的圆G相切,切点为T.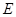 :
: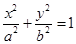 (
( )过点
)过点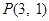 ,其左、右焦点分别为
,其左、右焦点分别为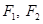 ,且
,且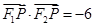 .
. 是直线
是直线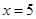 上的两个动点,且
上的两个动点,且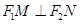 ,则以
,则以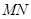 为直径的圆
为直径的圆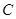 是否过定点?请说明理由.
是否过定点?请说明理由. :
: ,左、右两个焦点分别为
,左、右两个焦点分别为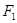 、
、 ,上顶点
,上顶点 ,
,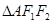 为正三角形且周长为6.
为正三角形且周长为6. 为坐标原点,
为坐标原点, 是直线
是直线 上的一个动点,求
上的一个动点,求 的最小值,并求出此时点
的最小值,并求出此时点 中,点
中,点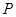 到两点
到两点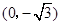 ,
, 的距离之和等于4,设点
的距离之和等于4,设点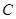 .
. 与
与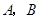 两点.k为何值时
两点.k为何值时
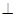
 ?此时
?此时 的值是多少?
的值是多少?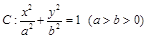 的左、右焦点分别为
的左、右焦点分别为 ,上顶点为
,上顶点为 ,离心率为
,离心率为 , 在
, 在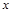 轴负半轴上有一点
轴负半轴上有一点 ,且
,且
 三点的圆 恰好与直线
三点的圆 恰好与直线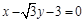 相切,求椭圆C的方程;
相切,求椭圆C的方程; 作斜率为
作斜率为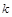 的直线
的直线 与椭圆C交于
与椭圆C交于 两点,在
两点,在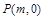 ,使得以
,使得以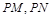 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由. (
( )的准线与
)的准线与 轴交于
轴交于 ,焦点为
,焦点为 ;以
;以 的椭圆
的椭圆 与抛物线
与抛物线 在
在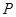 .
.
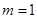 时,求椭圆的方程;
时,求椭圆的方程; 经过椭圆
经过椭圆 、
、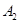 ,如果以线段
,如果以线段 为直径作圆,试判断点
为直径作圆,试判断点 ,使得
,使得 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数